Bài ôn tập chương I Động học chất điểm Sách bài tập Vật lí 10. Giải bài I.9, I.10, I.11, I.12, I.13 trang 22 Sách bài tập Vật lí 10. Câu I.9: Một ô tô và một xe máy xuất phát cùng một lúc từ hai địa điểm A và B cách nhau 20 km…
Bài I.9: Một ô tô và một xe máy xuất phát cùng một lúc từ hai địa điểm A và B cách nhau 20 km và chuyển động thẳng đều theo chiều từ A đến B. Ô tô đi từ A có vận tốc là 80 km/h và xe máy đi từ B có vận tốc là 40 km/h. Chọn A làm gốc toạ độ, chiều từ A đến B là chiều dương và chọn thời điểm xuất phát của hai xe làm mốc thời gian.
a) Viết phương trình chuyển động của mỗi xe.
b) Tính thời điểm và vị trí hai xe đuổi kịp nhau.
c) Vẽ đồ thị toạ độ – thời gian của hai xe. Căn cứ vào đồ thị này, hãy xác định vị trí và thời điểm hai xe đuổi kịp nhau. So sánh kết quả tìm được trên đồ thị với kết quả tính trong câu b).
a) Phương trình chuyển động của ô tô : xA = 80t
Phương trình chuyển động của xe máy : xB = 20 + 40t
b) Hai xe gặp nhau khi xA = xB. Từ đó suy ra :
– Thời điểm hai xe gặp nhau kể từ khi xuất phát : 80t = 20 + 40t
Hay \(t = {{20} \over {40}} = 0,5(h)\)
– Vị trí hai xe gặp nhau cách A một đoạn : xA = 80.0,5 = 40 km.
c) Đồ thị toạ độ của hai xe có dạng như trên hình I.1G, trong đó đường I biểu diễn chuyển động của ô tô và đường II biểu diễn chuyển động của xe máy.
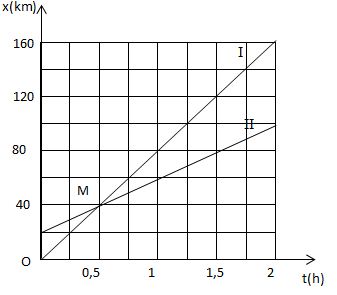
Căn cứ vào đồ thị trên hình I.l G, ta thấy hai đường biểu diễn I và II giao nhau tại điểm M ứng với thời điểm hai xe gặp nhau t = 0,5 giờ = 30 phút ở vị trí có toạ độ x = 40 km.
Như vậy kết quả tìm được trên đồ thị trùng với kết quả tính toán trong câu b).
Bài I.10: Một ô tô chuyển động thẳng nhanh dần đều đi qua điểm A rồi qua điểm B cách A 20 m trong thời gian t = 2 s. Vận tốc của ô tô khi đi qua điểm B là vB= 12 m/s.
a) Tính gia tốc của ô tô và vận tốc của nó khi đi qua điểm A.
b) Tính quãng đường ô tô đã đi được từ điểm khởi hành đến điểm A.
Chọn thời điểm ô tô đi qua điểm A làm mốc thời gian. Vì ô tô chuyển động thẳng nhanh dần đều nên gia tốc của ô tô được tính theo công thức : \(a = {{{v_B} – {v_A}} \over t}\) (1)
Mặt khác gia tốc a lại liên hệ với quãng đường đi được s và các vận tốc vA và vB theo công thức : \(v_B^2 – v_A^2 = 2as\)
a) Ta suy ra 2s = (vB + vA)t
hay \({v_A} = {{2s} \over t} – {v_B} = {{2.20} \over 2} – 12 = 8(m/s)\)
Advertisements (Quảng cáo)
Thay số vào (1) ta tính được gia tốc của ô tô : \(a = {{12 – 8} \over 2} = 2(m/{s^2})\)
b) Vì vận tốc đầu v0 = 0, nên quãng đường đi được của ô tô kể từ điểm khởi hành cho đến điểm A tính bằng : \({s_A} = {{at_A^2} \over 2}\)
Vì vA = a.tA nên suy ra:
\({s_A} = {{at_A^2} \over 2} = {a \over 2}{\left( {{{{v_A}} \over a}} \right)^2} = {{v_A^2} \over {2a}} = {{{8^2}} \over {2.2}} = 16(m)\)
Bài I.11: Một xe đạp đang đi với vận tốc 12 km/h thì hãm phanh. Xe chuyển động chậm dần đều và đi được thêm 10 m thì dừng lại.
a) Tính gia tốc của xe.
b) Tính thời gian hãm phanh.

a) Vận tốc xe đạp trước khi hãm phanh : v0 = 12 km/h = 10/3 (m/s)
Áp dụng công thức giữa vận tốc, gia tốc và quãng đường đi được: v2 – v02 = 2as với v = 0 và s = 10 m ;
ta tính được a = – 5/9 ≈ – 0,55 m/s2.
Vậy, gia tốc của xe đạp là – 0,55 m/s2.
b) Áp dụng công thức tính vận tốc v = v0 + at
ta tính được : t = 90/15 = 6 s.
Advertisements (Quảng cáo)
Vậy, thời gian hãm phanh là 6 giây.
Bài I.12: Một hòn bi lăn xuống một máng nghiêng theo đường thẳng. Khoảng cách giữa 5 vị trí liên tiếp A, B, C, D, E của hòn bi là AB = 3 cm, BC = 4 cm, CD = 5cm và DE = 6 cm. Khoảng thời gian để hòn bi lăn trên các đoạn AB, BC, CD và DE đều là 0,5 s.
a) Chứng minh chuyển động của hòn bi là chuyển động thẳng, nhanh dần đều.
b) Tính gia tốc của hòn bi.
a) Giả sử hòn bi chuyển động thẳng nhanh dần đều. Ta hãy tìm quy luật biến đổi của những quãng đường đi được liên tiếp trong những khoảng thời gian bằng nhau.
Đặt l1 = AB ; l2 = BC ; l3 = CD ; l4 = DE.
Gọi Δt là những khoảng thời gian bằng nhan liên tiếp mà hòn bi chuyển động trên các đoạn đường AB, BC, CD và DE.
Giả sử hòn bi xuất phát không vận tốc đầu từ điểm O và sau khoảng thời gian t nó lăn đến điểm A.
Gọi a là gia tốc của hòn bi, ta có \(OA = {1 \over 2}a{t^2}\) (1)
\(OB = {1 \over 2}a{(t + \Delta t)^2} = s + AB\) (2)
\(OC = {1 \over 2}a{(t + 2\Delta t)^2} = s + AB + BC\) (3)
\(OD = {1 \over 2}a{(t + 3\Delta t)^2} = s + AB + BC + CD\) (4)
\(OE = {1 \over 2}a{(t + 4\Delta t)^2} = s + AB + BC + CD + DE\) (5)
Lần lượt làm các phép trừ vế với vế các phương trình trên, ta có :
(2) – (1): \(AB = at\Delta t + {1 \over 2}a\Delta {t^2} = {l_1}\)
(3) – (2): \(BC = at\Delta t + {3 \over 2}a\Delta {t^2} = {l_2}\)
(4) – (3): \(CD = at\Delta t + {5 \over 2}a\Delta {t^2} = {l_3}\)
(5) – (4): \(DE = at\Delta t + {7 \over 2}a\Delta {t^2} = {l_4}\)
Từ các kết quả trên, ta rút ra nhận xét sau :
l2 – l1 = aΔt2; l3 – l2 = = aΔt2; l4 – l3 = = aΔt2
Vậy, trong chuyển động thẳng nhanh dần đều, hiệu những quãng đường đi được trong hai khoảng thời gian liên tiếp bằng nhau là một lượng không đổi.
Áp dụng vào bài toán này (AB = 3 cm, BC = 4 cm, CD = 5 cm và DE = 6 cm) ta thấy :
BC – AB = CD – BC = DE – CD = 1 cm
Vậy, chuyển động của hòn bi là chuyển động thẳng nhanh dần đều.
b) Từ phép tính trên ta rút ra công thức tính gia tốc của hòn bi là: \(a = {{{l_2} – {l_1}} \over {\Delta {t^2}}}\)
Với l2 – l1 = 1 cm ; Δt = 0,5 s ; ta có a = 4.10-2m/s2 = 4 cm/s2.
Bài I.13: Nếu có một giọt nước mưa rơi được 100 m trong giây cuối cùng trước khi chạm đất, thì giọt nước mưa đó phải bắt đầu rơi từ độ cao bao nhiêu mét ? Cho rằng chuyển động của giọt nước mưa là rơi tự do với g = 9,8 m/s2 và trong suốt quá trình rơi, khối lượng của nó không bị thay đổi.
Gọi s là quãng đường rơi của giọt nước mưa từ lúc đầu đến điểm cách mặt đất 100 m, t là thời gian rơi trên quãng đường đó, ta có : \(s = {1 \over 2}g{t^2}\) (1)
Mặt khác, quãng đường rơi từ lúc đầu đến mặt đất là s + 100 và thời gian rơi trên quãng đường đó là t + 1 giây.
Ta có :\(s + 100 = {1 \over 2}g{(t + 1)^2}\) (2)
Từ hai phương trình (1) và (2) ta rút ra : \(t = {{100} \over 9} – 0,5 \approx 9,7(s) = > s = 461(m)\)
Vậy, độ cao ban đầu của giọt nước mưa lúc bắt đầu rơi là:
s +100 = 561 m.

