Bài 2.25, 2.26, 2.27, 2.28 trang 92 SBT Toán Hình học 10: Chứng minh ba điểm A, B, C không thẳng hàng ?

Bài 2.25: Trong mặt phẳng Oxy cho bốn điểm A( – 1;1), B(0;2), C(3;1) và D(0;-2). Chứng minh rằng tứ giác ABCD là hình thang cân.

Ta có: \(\overrightarrow {AB}  = (1;1),\,\,\overrightarrow {DC}  = (3;3)\)

Vậy \(\overrightarrow {DC}  = 3\overrightarrow {AB} \), ta suy ra DC // AB và DC = 3AB.

Mặt khác \(\left| {\overrightarrow {AD} } \right| = \sqrt {{1^2} + {3^2}} \) và \(\left| {\overrightarrow {BC} } \right| = \sqrt {{3^2} + {1^2}} \)

Nên ABCD là hình thang cân có hai cạnh bên AD và BC bằng nhau, còn hai đáy là AB và CD trong đó đáy lớn CD dài gấp 3 lần đáy nhỏ AB.

Bài 2.26: Trong mặt phẳng Oxy cho ba điểm A( – 1; – 1), B(3;1) và C(6;0). 

a) Chứng minh ba điểm A, B, C không thẳng hàng.

b) Tính góc B của tam giác ABC.

a) Ta có: \(\overrightarrow {AB}  = (4;2),\overrightarrow {AC}  = (7;1)\)

Vì \({4 \over 7} \ne {2 \over 1}\) nên ba điểm A, B, C không thẳng hàng.

b) Ta có \(\cos B = \cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = {{\overrightarrow {BA} .\overrightarrow {BC} } \over {\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}}\) với \(\overrightarrow {BA}  = ( – 4; – 2),\overrightarrow {BC}  = (3; – 1)\)

Do đó:

\(\eqalign{
& \cos B = {{( – 4.3) + ( – 2)( – 1)} \over {\sqrt {16 + 4} .\sqrt {9 + 1} }} \cr
& = {{ – 10} \over {\sqrt {200} }} = – {{\sqrt 2 } \over 2} \cr} \)

Vậy \(\widehat B = {135^0}\)

Bài 2.27: Trong mặt phẳng Oxy cho hai điểm A(5;4) và B(3;-2). Một điểm M di động trên trục hoành Ox. Tìm giá trị nhỏ nhất của \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right|\)

(h.2.28)

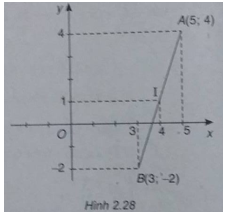
Gọi I là trung điểm của đoạn AB, ta có I(4;1)

Vì \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \) nên \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = 2\left| {\overrightarrow {MI} } \right|\) nhỏ nhất khi giá trị của đoạn IM nhỏ nhất. Điểm M chạy trên trục Ox nên có tọa độ dạng M(x; 0). Do đó:

\(\left| {\overrightarrow {IM} } \right| = \sqrt {{{(x – 4)}^2} + 1}  \ge 1\)

Dấu “=” xảy ra khi x = 4.

Vậy giá trị nhỏ nhất của \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right|\) là 2 khi M có tọa độ là M(4;0)

Bài 2.28: Trong mặt phẳng Oxy cho bốn điểm A(3;4), B(4;1), C(2; – 3), D( – 1;6). Chứng minh tứ giác ABCD nội tiếp được trong một đường tròn.

Muốn chứng minh tứ giác ABCD nội tiếp được trong một đường tròn, ta chứng minh tứ giác này có hai góc đối bù nhau. Khi đó hai góc này có cô sin đối nhau.

Theo giả thiết ta có:

\(\eqalign{
& \overrightarrow {AB} = (1; – 3),\overrightarrow {AD} = ( – 4;2), \cr
& \overrightarrow {CB} = (2;4);\overrightarrow {CD} = ( – 3;9) \cr} \)

Do đó:

\(\eqalign{
& \cos (\overrightarrow {AB} ,\overrightarrow {AD} ) = {{\overrightarrow {AB} .\overrightarrow {AD} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|}} \cr
& = {{1.( – 4) + ( – 3).2} \over {\sqrt {1 + 9} .\sqrt {16 + 4} }} = {{ – 10} \over {\sqrt {200} }} = – {1 \over {\sqrt 2 }} \cr} \)

\(\eqalign{
& \cos (\overrightarrow {CB} ,\overrightarrow {AD} ) = {{\overrightarrow {CB} .\overrightarrow {CD} } \over {\left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {CD} } \right|}} \cr
& = {{2.( – 3) + 4.9} \over {\sqrt {4 + 16} .\sqrt {9 + 81} }} = {{30} \over {\sqrt {1800} }} = {1 \over {\sqrt 2 }} \cr} \)

Vì \(\cos (\overrightarrow {AB} ,\overrightarrow {AD} ) =  – \cos (\overrightarrow {CB} ,\overrightarrow {CD} )\) nên hai góc này bù nhau. Vậy tứ giác ABCD nội tiếp được trong một đường tròn.