Bài 20: Hai hàm số y = x + 4 và \(y = {{{x^2} – 16} \over {x – 4}}\) có chung một tập xác định hay không ?
 Không.
Không.
Vì Hàm số y = x + 4 TXĐ: D = R
Hàm số TXĐ: \(y = {{{x^2} – 16} \over {x – 4}}\) D = R\{4}
Bài 21: Cho hàm số y = f(x) nghịch biến trên khoảng (a ;b), khi đó hàm số y =-f(x) có chiều biến thiên như thế nào trên khoảng (a ; b) ?

Do hàm số \(y = f(x)\) nghịch biến trên khoảng (a;b) nên
\(\eqalign{
& \forall x_1^{} < x_2^{} \in \left( {a;b} \right):f(x_1^{}) > f(x_2^{}) \cr
& \Leftrightarrow – f(x_1^{}) < – f(x_2^{}) \cr} \)
Vậy hàm số \)y = – f(x)\) đồng biến trên khoảng (a;b).
Bài 22: Tìm giao điểm của parabol \(y = 2{x^2} + 3x – 2\) với các đường thẳng
a) y = 2x + 1 ;
Advertisements (Quảng cáo)
b) y = x – 4 ;
c) y = -x – 4 ;
d) y = 3.
Hướng dẫn. Để xác định hoành độ giao điểm của hai đồ thị có phương trình tương ứng là và ta phải giải phương trình \(f(x) = g(x)\)

a) Xét phương trình:
Advertisements (Quảng cáo)
\(2{x^2} + 3x – 2 = 2x + 1 \Leftrightarrow 2{x^2} + x – 3 = 0 \Leftrightarrow \left[ \matrix{
{x_1} = 1 \hfill \cr
{x_2} = – {3 \over 2} \hfill \cr} \right.\)
Vậy parabol đã cho và đường thẳng y = 2x + 1 có hai giao điểm là (1;3) và \(( – {3 \over 2}; – 2)\)
b) Xét phương trình \(2{x^2} + 3x – 2 = x – 4\)
\(\eqalign{
& \Leftrightarrow 2{x^2} + 2x + 2 = 0 \cr
& \Leftrightarrow 2{x^2} + 2x + 2 = 0 \cr
& \Leftrightarrow {x^2} + x + 1 = 0(*) \cr} \)
Phương trình (*) có biệt thức \(\Delta = 1 – 4 = – 3 < 0\) , do đó phương trình vô nghiệm.
Vậy parabol đã cho và đường thẳng y = x – 4 không có giao điểm.
c) Xét phương trình
\(2{x^2} + 3x – 2 = – x – 4 \Leftrightarrow 2{x^2} + 4x + 2 = 0\)
\({x^2} + 2x + 1 = 0 = > x = – 1\)
Vậy parabol đã cho và đường thẳng y = -x – 4 tiếp xúc nhau tại điểm có tọa độ (-1;-3).
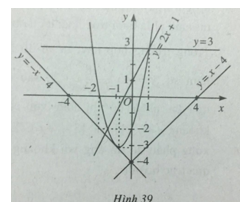
Đồ thị được vẽ trên hình 39
d) Xét phương trình
\(2{x^2} + 3x – 2 = 3 \Leftrightarrow 2{x^2} + 3x – 5 = 0 \Leftrightarrow \left[ \matrix{
{x_1} = 1 \hfill \cr
{x_2} = – {5 \over 2} \hfill \cr} \right.\)
Vậy có hai giao điểm là (1;3) và \(( – {5 \over 2};3)\)

