Bài 3 Hàm số bậc hai SBT Toán Đại số lớp 10. Giải bài 17, 18, 19 trang 40 Sách bài tập Toán Đại số 10. Câu 17: Viết phương trình của parabol …
Bài 17: Viết phương trình của parabol \(y = a{x^2} + bx + c\) ứng với mỗi đồ thị dưới đây
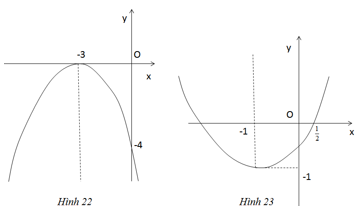

a) Dựa trên đồ thị (h.22) tâ thấy parabol có đỉnh I(-3 ;0) và đi qua điểm (0 ;-4). Như vậy
\(c = – 4; – {b \over {2a}} = – 3 \Leftrightarrow b = 6a\) Thay c = -4 và b = 6a vào biểu thức
\(\Delta = {b^2} – 4ac = 0 = > 36{a^2} + 16a = 0 = > a = – {4 \over 9}\) (vì \(a \ne 0)\) và \(b = – {8 \over 3}\)
Vậy phương trình của parabol là \(y = – {4 \over 9}{x^2} – {8 \over 3}x – 4\)
Advertisements (Quảng cáo)
b) \(y = {4 \over 9}{x^2} + {8 \over 9}x – {5 \over 9}\)
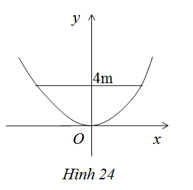
Bài 18: Một chiếc ăng – ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4 m. Ở mặt cắt qua trục ta được một parabol dạng \(y = a{x^2}\) (h.24). Hãy xác định hệ số a.
Advertisements (Quảng cáo)

Ta có thiết diện mặt cắt qua trục của chiếc ăng-ten là:
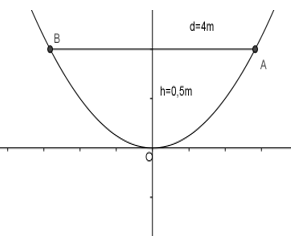
Vậy ta có: \(A\left( {2;{1 \over 2}} \right)\) mà \(A \in \) prapol: \(y = ax_{}^2\) \( \Rightarrow {1 \over 2} = a.2_{}^2 \Leftrightarrow a = {1 \over 8}\)
Bài 19: Một chiếc cổng hình parabol dạng \(y = – {1 \over 2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).
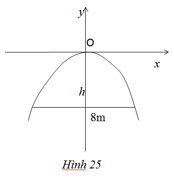

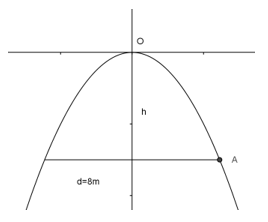
Ta có: \(A\left( {4; – h} \right)\) mà \(A \in \) parabol \(y = – {1 \over 2}x_{}^2\) \( \Rightarrow h = \left| { – {1 \over 2}.4_{}^2} \right| \Rightarrow h = 8\)

