Bài 14: Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.
a) \(y = 2{x^2} – x – 2\)
b) \(y = – 2{x^2} – x + 2\)
c) \(y = – {1 \over 2}{x^2} + 2x – 1\)
d) \(y = {1 \over 5}{x^2} – 2x + 6\)

a) Ở đây \(a = 2;b = – 2;c = – 2\) . Ta có \(\Delta = {( – 1)^2} – 4.2.( – 2) = 17\)
Trục đối xứng là đường thẳng \(x = {1 \over 4}\) ; đỉnh \(I({1 \over 4}; – {{17} \over 8})\) giao với trục tung tại điểm (0;-2).
Để tìm giao điểm với trục hoành ta giải phương trình
\(2{x^2} – x – 2 = 0 \Leftrightarrow {x_{1,2}} = {{1 \pm \sqrt {17} } \over 4}\)
Vậy các giao điểm với trục hoành là \(({{1 + \sqrt {17} } \over 4};0)\) và \(({{1 – \sqrt {17} } \over 4};0)\)
b) Trục đối xứng \(x = – {1 \over 4}\) ; đỉnh \(I( – {1 \over 4}; – {{17} \over 8})\) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm \(( – {{1 + \sqrt {17} } \over 4};0)\) và \(({{\sqrt {17} – 1} \over 4};0)\) .
c) Trục đối xứng x = 2; đỉnh I(2;1); giao với trục tung tại điểm (0;-1) giao với trục hoành tại các điểm \((1 + \sqrt 2 ;0)\) và \((2 – \sqrt 2 ;0)\)
d) Trục đối xứng x = 5; đỉnh I(5;1); giao với trục tung tại điểm (0;6). Parabol không cắt trục hoành \((\Delta = – {4 \over 5} < 0)\)
Bài 15: Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
a) \(y = 2{x^2} + 4x – 6\)
b) \(y = – 3{x^2} – 6x + 4\)
c) \(y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2\)
d) \(y = – 2({x^2} + 1)\)
Advertisements (Quảng cáo)

a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;
Vậy \( – {b \over {2a}} = – 1;\Delta = {b^2} – 4ac = 64; – {\Delta \over {4a}} = – 8\)
Vì a > 0, ta có bảng biến thiên
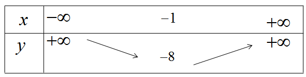
Hàm số nghịch biến trên khoảng \(( – \infty ; – 1)\) đồng biến trên khoảng \(( – 1; + \infty )\)
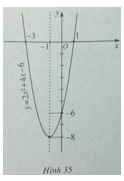
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).
Đồ thị của hàm số \(y = 2{x^2} + 4x – 6\) được vẽ trên hình 35.
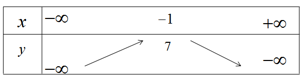
b) Bảng biến thiên
Advertisements (Quảng cáo)
Hàm số đồng biến trên khoảng \(( – \infty ; – 1)\) và nghịch biến trên khoảng \(( – 1; + \infty )\)
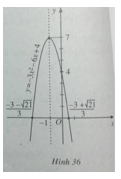
Đỉnh parabol I(-1;7). Đồ thị của hàm số \(y = – 3{x^2} – 6x + 4\) được vẽ trên hình 36.
c) Bảng biến thiên
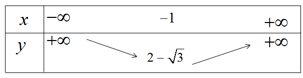
Hàm số nghịch biến trên khoảng \(( – \infty ; – 1)\) và đồng biến trên khoảng \(( – 1; + \infty )\)
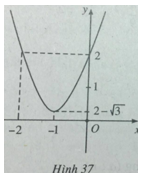
Đỉnh parabol \(( – 1;2 – \sqrt 3 )\)
Đồ thị hàm số được vẽ trên hình 37.
d) \(y = – 2{x^2} – 2\)
Bảng biến thiên
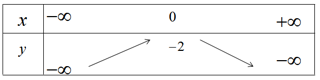
Hàm số đồng biến trên khoảng \(( – \infty ;0)\) và nghịch biến trên khoảng \((0; + \infty )\) , hàm số là chẵn.
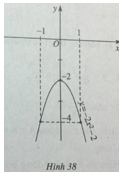
Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).
Đồ thị hàm số \(y = – 2({x^2} + 1)\) được vẽ trên hình 38.
Bài 16: Xác định hàm số bậc hai \(y = a{x^2} – 4x + c\), biết rằng đồ thị của nó
a) Đi qua hai điểm A(1;-2) và B(2;3);
b) Có đỉnh là I(-2 ;-1) ;
c) Có hoành độ đỉnh là -3 và đi qua điểm P(-2 ;1) ;
d) Có trục đối xứng là đường thẳng x = 2 và cắt trục hoành tại điểm M(3 ;0).

Các hàm số bậc hai cần xác định đều có b = -4.
a) Ta có
\(\left\{ \matrix{
– 2 = a – 4 + c \hfill \cr
3 = 4a – 8 + c \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a + c = 2 \hfill \cr
4a + c = 11 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 3 \hfill \cr
c = – 1 \hfill \cr} \right.\)
Vậy hàm số cần tìm là \(y = 3{x^2} – 4x – 1\)
b) \(y = – {x^2} – 4x – 5\)
c) \(y = – {2 \over 3}{x^2} – 4x – {{13} \over 3}\)
d) \(y = {x^2} – 4x + 3\)

