Câu 36: Cho nửa đường tròn đường kính AB cố định. C là điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB.
a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.
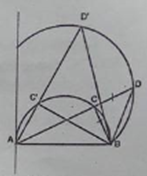
b) Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho.
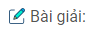
a) Chứng minh thuận:
Ta có: \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra: \(\widehat {BCD} = 90^\circ \)
CD = CB (gt)
Suy ra: ∆BCD vuông cân tại C.
\( \Rightarrow \widehat {CDB} = 45^\circ \) hay \(\widehat {ADB} = 45^\circ \)
AB cố định. Khi C chuyển động trên nửa đường tròn đường kính AB thì D chuyển động trên cung chứa góc 45º dựng trên đoạn thẳng AB cố định.
Ta có dây AC thay đổi phụ thuộc vào vị trí điểm C trên nửa đường tròn đường kính AB.
− Dây AC lớn nhất bằng đường kính của đường tròn. Khi C trùng với B khi đó D trùng với B. Vậy B là điểm của quỹ tích.
− Dây AC nhỏ nhất có độ dài bằng 0 khi C trùng với A, thì khi đó D trùng ới B’ là giao điểm của tiếp tuyến đường tròn đường kính AB tại A với cung chứa góc 45º vẽ trên AB.
Chứng minh đảo: Lấy điểm D’ tùy ý trên cung BB’, nối AD’ cắt đường tròn đường kính AB tại C’. Nối BC’, B’D’.
Ta có: \(\widehat {AD’B} = 45^\circ \) (vì D’ nằm trên cung chứa góc 45º vẽ trên AB).
Trong đường tròn đường kính AB ta có:
\(\widehat {AC’B} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \widehat {BC’D’} = 90^\circ \)
Suy ra: ∆BC’D’ vuông cân tại C’
\( \Rightarrow \) C’B = C’D’
Vậy quỹ tích các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là cung \(\overparen{BB’}\) nằm trên cung chứa góc 45º vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C.
b) Chứng minh thuận:
Trong đường tròn đường kính AB ta có:
Advertisements (Quảng cáo)
\(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
CB = CE (gt)
\( \Rightarrow \) ∆CBE vuông tại C
\( \Rightarrow \widehat {CEB} = 45^\circ \)
\(\widehat {CEB} + \widehat {AEB} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {AEB} = 135^\circ \)
AB cố định, C chuyển động trên đường tròn đường kính AB thì E chuyển động trên cung chứa góc 135º dựng trên đoạn AB cố định.
− Khi dây AC có độ dài lớn nhất bằng đường kính đường tròn, thì C trùng với B nên E trùng với B \( \Rightarrow \) B là 1 điểm của quỹ tích.
− Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A. Khi đó E trùng A nên A là 1 điểm của quỹ tích.
Vậy E chuyển động trên 1 cung chứa góc 135º vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C.
Chứng minh đảo: Lấy E’ bất kỳ trên cung chứa góc 135º. Kẻ AE’ cắt đường tròn đường kính AB tại C’. Nối BE’, BC’.
Ta có: \(\widehat {AE’B} = 135^\circ \) (vì E’ nằm trên cung chứa góc 135º)
\(\widehat {AE’B} + \widehat {BE’C} = 180^\circ \) (kề bù)
\( \Rightarrow \widehat {BE’C’} = 180^\circ – \widehat {AE’B} = 180^\circ – 135^\circ = 45^\circ \)
Trong đường tròn đường kính AB ta có:
\(\widehat {AC’B} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Advertisements (Quảng cáo)
Suy ra: ∆E’C’B vuông cân tại C’. \( \Rightarrow \) C¢E¢ = C¢B
Vậy quỹ tích các điểm E khi C chuyển động trên đường tròn đường kính AB là một cung chứa góc 135º vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C.
Câu 37: Cho nửa đường tròn đường kính AB và C là một điểm trên nửa đường tròn. Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách CH từ C đến AB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.
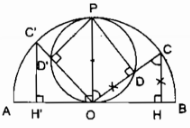
Chứng minh thuận:
Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P. O cố định, đường tròn đường kính AB cố định suy ra P cố định.
Nối PD. Ta có: OP // CH (vì hai đường thẳng cùng vuông góc với AB)
Xét ∆OCH và ∆OPD:
OD = CH (gt)
OP = OC (bán kính)
\(\widehat {POD} = \widehat {OCH}\) (so le trong)
Suy ra: ∆DOP = ∆HCO (c.g.c)
\( \Rightarrow \)\(\widehat {ODP} = \widehat {CHO}\) mà \(\widehat {CHO} = 90^\circ \) nên \(\widehat {ODP} = 90^\circ \)
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với 2 đầu đoạn thẳng OP cố định một góc \(\widehat {OPD} = 90^\circ \). Vậy D chuyển động trên đường tròn đường kính OP.
Chứng minh đảo: Lấy điểm D¢ bất kỳ trên đường tròn đường kính OP. Kẻ OD’ cắt nửa đường tròn đường kính AB tại C’, kẻ C’H’⊥ AB ta phải chứng minh OD’ = C’H’.
Nối PD’. Xét ∆C’H’O và ∆PD’O
\(\widehat {C’H’O} = \widehat {PD’O} = 90^\circ \)
OC’ = OP (bán kính đường tròn tâm O)
\(\widehat {D’OP} = \widehat {OC’H’}\) (so le trong)
Suy ra: ∆C’H’O = ∆PD’O (cạnh huyền, góc nhọn)
\( \Rightarrow \) C’H’ = OD’
Vậy quỹ tích các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP.
Câu 38: Dựng hình vuông ABCD, biết đỉnh A, điểm M thuộc cạnh BC và điểm N thuộc cạnh CD.
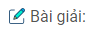
Phân tích: Giả sử hình vuông ABCD dung được thỏa mãn điều kiện bài toán. Ta cần dựng đỉnh C. Đỉnh C thỏa mãn 2 điều kiện:
− \(\widehat {MCN} = 90^\circ \) nên C nằm trên cung chứa góc 90º dựng trên MN.
− Ta có \(\widehat {ACM} = 45^\circ \) (vì hình vuông có đường chéo là phân giác) nên C nằm trên cung chứa góc 45º vẽ trên AM.
Cách dựng: − Dựng cung chứa góc 90º trên đoạn MN.
− Dựng cung chứa góc 45º trên đoạn AM.
Hai cung cắt nhau tại C, nối CM, CN.
Kẻ AB ⊥ CN tại B, AD ⊥ CN tại D.
Ta có tứ giác ABCD là hình vuông cần dựng.
Chứng minh: Thật vậy theo cách dựng ta có: \(\widehat C = 90^\circ ,\widehat B = 90^\circ ,\widehat D = 90^\circ \)
Tứ giác ABCD là hình chữ nhật, có điểm M thuộc BC, điểm N thuộc CD. AC là phân giác của \(\widehat C.\)
Vậy: tứ giác ABCD là hình vuông.

