Câu 18: Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B. Chứng minh rằng tích MA.MB không đổi.
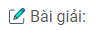
Trường hợp M ở bên trong đường tròn (O)
Kẻ cát tuyến AB bất kỳ và kẻ đường thẳng MO cắt đường tròn tại C và D.
Xét hai ∆MAC và ∆MBD:
\(\widehat {AMC} = \widehat {BMD}\) (đối đỉnh)
\(\widehat A = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{BC}\)
Suy ra: ∆MAC đồng dạng ∆MDB (g.g)
\( \Rightarrow {{MB} \over {MC}} = {{MD} \over {MA}}\)
\( \Rightarrow MA.MB = MC.MD\) (1)
Vì M, O cố định suy ra điểm C và D cố định nên độ dài của các đoạn MC và MD không đổi \( \Rightarrow \) tích MC.MD không đổi (2)
Từ (1) và (2) suy ra tích MA. MB không đổi khi cát tuyến AB thay đổi.
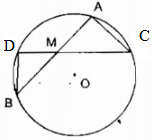
Trường hợp điểm M ở ngoài đường tròn (O)
Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D
Xét ∆MAD và ∆MCB:
\(\widehat M\) chung
\(\widehat B = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{AC}\))
Suy ra: ∆MAD đồng dạng ∆MCB (g.g)
\( \Rightarrow {{MC} \over {MA}} = {{MB} \over {MD}} \Rightarrow MA.MB = MC.MD\) (3)
Vì M và O cố định suy ra điểm C, D cố định nên độ dài của các đoạn MC và MD không đổi \( \Rightarrow \) tích MC. MD không đổi (4)
Advertisements (Quảng cáo)
Từ (3) và (4) suy ra tích MA. MB không đổi khi cát tuyến MAB thay đổi.
Câu 19: Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình 1). Biết chiều rộng của đường ray là AB \( \approx 1,1m\), đoạn BC \( \approx 28,4m\). Hãy tính bán kính OA = R của đoạn đường ray hình vòng cung.
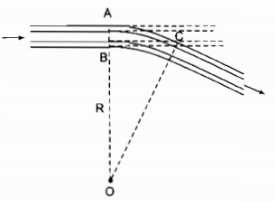
Ta xem hai đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung.
Điểm B cố định nằm trong đường tròn có cung \(\overparen{AC}\).
Đường thẳng OB cắt đường tròn đó tại A và A’.
A cố định và A’ cố định
B là tiếp điểm cung nhỏ trong nên BC là tiếp tuyến của đường tròn (O; OB)
\( \Rightarrow BC \bot OB\). Kéo dài BC cắt đường tròn (O; OA) tại C’
\( \Rightarrow BC = BC’\) (đường kính vuông góc dây cung)
Xét ∆BAC và ∆BA’C:
\(\widehat {ABC} = \widehat {C’BA’}\) (đối đỉnh)
\(\widehat {ACB} = \widehat {C’A’B}\) (2 góc nội tiếp cùng chắn cung \(\overparen{AC’}\))
Advertisements (Quảng cáo)
Suy ra: ∆BAC đồng dạng ∆BC’A’ (g.g)
\( \Rightarrow {{BC’} \over {AB}} = {{BA’} \over {BC}}\)
\( \Rightarrow BC.BC’ = AB.BA’\) mà BC = BC’; BA’ = 2R – AB
Suy ra: \(B{C^2} = AB\left( {2R – AB} \right)\)
\({\left( {28,4} \right)^2} \approx 1,1.\left( {2R – 1,1} \right)\)
\( \Rightarrow 2,2R \approx 806,56 + 1,21\)
\(R \approx 807,77:2,2 = 367,2\) (m).
Câu 20: Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm của cung nhỏ BC. Trên MA lấy điểm D sao cho MD = MB.
a) Hỏi tam giác MBD là tam giác gì?
b) So sánh hai tam giác BDA và BMC.
c) Chứng minh rằng MA = MB + MC.
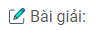
a) MB = MD (gt) \( \Rightarrow \) ∆MBD cân tại M
\(\widehat {AMB} = \widehat {ACB}\) (2 góc nội tiếp cùng chắn cung \(\overparen{AB}\))
Mà \(\widehat {ACB} = {60^0}\) (vì ∆ABC đều)
\( \Rightarrow \widehat {AMB} = {60^0}\) hay \(\widehat {DMB} = {60^0}\)
Vậy ∆MBD đều
b) ∆MBD đều
\( \Rightarrow \widehat {DBC} + \widehat {CBM} = \widehat {DBM} = {60^0}\) (1)
∆ABC đều \( \Rightarrow \widehat {ABD} + \widehat {DBC} = \widehat {ABC} = {60^0}\) (2)
Từ (1) và (2) suy ra: \(\widehat {CBM} = \widehat {ABD}\)
Xét ∆BDA và ∆BMC:
BA = BC (gt)
\(\widehat {ABD} = \widehat {CBM}\) (chứng minh trên)
BD = BM (vì ∆MBD đều)
Suy ra: ∆BDA = ∆BMC (c.g.c)
c) ∆BDA = ∆BMC (chứng minh trên)
\( \Rightarrow DA = MC\)
Ta có: MB = MD (gt) mà AM = AD + DM
Suy ra: MA = MD + MC.

