Câu 64: Tính diên tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 100\(^\circ \).

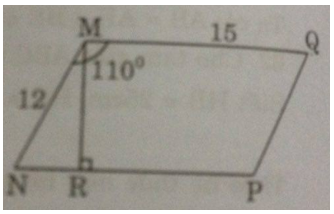
Giả sử hình bình hành MNPQ có MN = 12cm, MQ = 15cm, \(\widehat {NMQ} = 110^\circ \)
Ta có: \(\widehat {NMQ} + \widehat {MNP} = 180^\circ \) (hai góc trong cùng phía)
Suy ra: \(\widehat {MNP} = 180^\circ – \widehat {NMQ}\)
\( = 180^\circ – 110^\circ = 70^\circ \)
Kẻ \(MR \bot NP\)
Trong tam giác vuông MNR, ta có:
\(\eqalign{
& MR = MN.\sin \widehat {MNP} \cr
& = 12.\sin 70^\circ \approx 11,276\,(cm) \cr} \)
Vậy \({S_{MNPQ}} = MN.NP \approx 11,276.15 = 169,14\) (cm2).
Câu 65: Tính diện tích hình thang cân, biết hai cạnh đáy là 12cm và 18cm, góc ở đáy bằng 75\(^\circ \)

Advertisements (Quảng cáo)
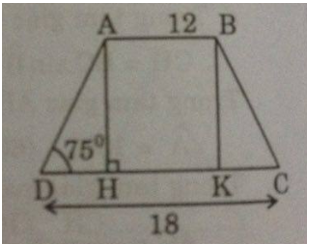
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, \(\widehat D = 75^\circ \)
Kẻ \(AH \bot CD,BK \bot CD\)
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
\(DH = {{CD – HK} \over 2} = {{18 – 12} \over 2} = 3\,(cm)\)
Advertisements (Quảng cáo)
Trong tam giác vuông ADH, ta có:
\(AH = DH.tgD = 3.tg75^\circ \approx 11,196\,(cm)\)
Vậy:
\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr
& \approx {{12 + 18} \over 2}.11,196 = 167,94 \cr} \) (cm2).
Câu 66: Một cột cờ cao 3,5m có bóng trên mặt đất dài 4,8m. Hỏi góc giữa tia sáng mặt trời và bóng cột cờ là bao nhiêu?

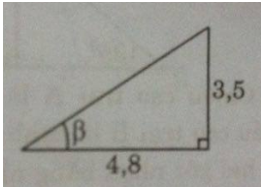
Chiều cao cột cờ là cạnh đối diên với góc giữa tia sang mặt trời và bóng cột cờ, chiều dài bóng là cạnh kề góc nhọn.
Ta có: \(tg\beta = {{3,5} \over {4,8}} = {{35} \over {48}}\)
Suy ra: \(\beta = 36^\circ 6’\)
Câu 67: Từ đỉnh một tòa nhà cao 60m, người ta nhìn thấy một chiếc ô tô đang đỗ dưới một góc 28\(^\circ \) so với đường nằm ngang. Hỏi chiếc ô tô đang đỗ cách tòa nhà đó bao nhiêu mét?

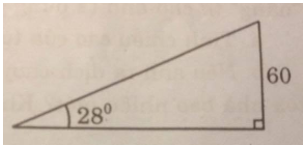
Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28\(^\circ \), chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
\(60.\cot g28^\circ \approx 112,844\,(m)\)

