Câu 68: Một em học sinh đứng ở mặt đất cách tòa tháp ăng-ten 150m. Biết rằng em nhìn thấy đỉnh tháp ở góc 20\(^\circ \) so với đường nằm ngang, khoảng cách từ mắt đến mặt đất bằng 1,5m. Hãy tính chiều cao của tháp.

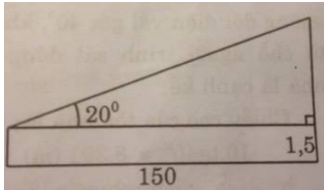
Phần còn lại của cột ăng-ten là cạnh đối của góc 20\(^\circ \), khoảng cách từ chỗ em đứng đến chân cột ăng-ten là cạnh kề với góc 20\(^\circ \).
Phần còn lại của cột ăng-ten cao là:
\(150.tg20^\circ \approx 54,596\,(m)\)
Chiều cao của cột ăng-ten là:
54,596 + 1,5 = 56,096 (m).
Câu 69: Hai cột thẳng của hai trại A và B, của lớp 9A và lớp 9B, cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35\(^\circ \) và 30\(^\circ \) (h.23). Hỏi trại nào cao hơn và cao hơn bao nhiêu mét?

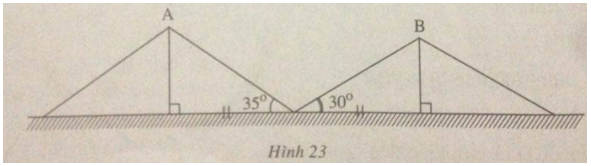
Chiều cao trại A là cạnh góc vuông đối diện với góc nhọn 35\(^\circ \), chiều cao trại B là cạnh góc vuông đối diện với góc nhọn 30\(^\circ \), cạnh kề với hai góc nhọn bằng nhau bằng 4m.
Chiều cao trại A là: \(4.tg35^\circ \approx 2,801\,(m)\)
Chiều cao trại B là: \(4.tg30^\circ \approx 2,309\,(m)\)
Trại A cao hơn trại B là: \(2,801 – 2,309 = 0,492\,(m)\)
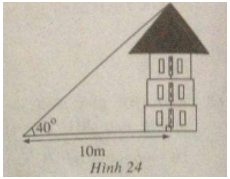
Câu 70: Một người trinh sát đứng cách một tòa nhà một khoảng 10m. Góc “nâng” từ chỗ anh ta đứng đến nóc nhà là 40\(^\circ \) (h.24).
Advertisements (Quảng cáo)
a) Tính chiều cao của tòa nhà.
b) Nếu anh ta dịch chuyển sao cho góc “nâng” là 35\(^\circ \) thì anh ta cách tòa nhà bao nhiêu mét? Khi đó anh ta tiến lại gần hay ra xa ngôi nhà?

a) Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40\(^\circ \) , khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.
Chiều cao của tòa nhà là:
\(10.tg40^\circ \approx 8,391\,(m)\)
b) Nếu dịch chuyển sao cho góc “nâng” là 35\(^\circ \) thì anh ta cách tòa nhà:
\(8,391.\cot g35^\circ \approx 11,934\,(m)\)
Câu 71: Một chiếc diều ABCD có AB = BC, AD = DC. Biết \(AB = 12cm,\widehat {ADC} = 40^\circ \)
\(\widehat {ABC} = 90^\circ \) (h.25)
Advertisements (Quảng cáo)
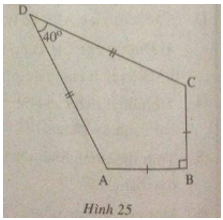
Hãy tính:
a) Chiều dài cạnh AD;
b) Diện tích của chiếc diều.

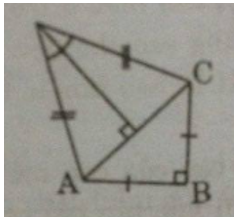
a) Nối AC và kẻ \(DH \bot AC\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} \cr
& = {12^2} + {12^2} = 144 + 144 = 288 \cr} \)
Suy ra: \(AC = 12\sqrt 2 \,(cm)\)
Ta có: tam giác ACD cân tại D
\(DH \bot AC\)
Suy ra: \(HA = HC = {{AC} \over 2} = 6\sqrt 2 \,(cm)\)
\(\widehat {ADH} = {1 \over 2}\widehat {ADC} = 20^\circ \)
Trong tam giác vuông ADH, ta có:
\(\eqalign{
& {\rm{AD = }}{{AH} \over {\sin \widehat {ADH}}} \cr
& = {{6\sqrt 2 } \over {\sin 20^\circ }} \approx 24,809\,(cm) \cr} \)
b) Ta có:
\({S_{ABC}} = {1 \over 2}.AB.BC = {1 \over 2}.12.12 = 72\,\) (cm2)
Trong tam giác vuông ADH, ta có:
\(\eqalign{
& DH = AH.\cot g\widehat {ADH} \cr
& = 6\sqrt 2 .\cot g20^\circ \approx 23,313\,(cm) \cr} \)
Mặt khác:
\(\eqalign{
& {S_{ADC}} = {1 \over 2}.DH.AC \cr
& \approx {1 \over 2}.23,313.12\sqrt 2 = 197,817 \cr} \) (cm2)
Vậy Sdiều \(\eqalign{
& = {S_{ABC}} + {S_{ADC}} \cr
& = 72 + 197,817 = 269,817 \cr} \) (cm2)

