Câu 60: Cho hình

Biết:
\(\widehat {QPT} = 18^\circ \),
\(\widehat {PTQ} = 150^\circ \),
QT = 8cm,
TR = 5cm.
Hãy tính:
a) PT;
b) Diện tích tam giác PQR.


a) Kẻ \(QS \bot PR\)
Ta có: \(\widehat {QTS} = 180^\circ – \widehat {QTP} = 180^\circ – 150^\circ = 30^\circ \)
Trong tam giác vuông QST, ta có:
\(QS = QT.\sin \widehat {QTS} = 8.\sin 30^\circ = 4\left( {cm} \right)\)
\(TS = QT.c{\rm{os}}\widehat {QTS} = 8.c{\rm{os30}}^\circ \approx 6,928\left( {cm} \right)\)
Trong tam giác vuông QSP, ta có:
\(SP = QS.\cot g\widehat {QPS} = 4.\cot g18^\circ = 12,311\left( {cm} \right)\)
\(PT = SP – TS \approx 12,311 – 6,928 = 5,383\left( {cm} \right)\)
b) Ta có:
\({S_{\Delta QPR}} = {1 \over 2}.QS.PR = {1 \over 2}.QS.(PT + TR)\)
Advertisements (Quảng cáo)
\( \approx {1 \over 2}.4.(5,383 + 5) = {1 \over 2}.10,383 = 20,766\left( {c{m^2}} \right)\)
Câu 61: Cho BCD là tam giác đều cạnh 5cm và góc DBA bằng 40°.

Hãy tính:
a) AD;
b) AB.

a) Kẻ \(DE \bot BC\)
Suy ra: \(BE = EC = {1 \over 2}BC = 2,5\left( {cm} \right)\)
Trong tam giác vuông BDE, ta có:
\(DE = BD.\sin \widehat {DBE} = 2,5.\sin 60^\circ = {{5\sqrt 3 } \over 2}\left( {cm} \right)\)
Trong tam giác vuông ADE, ta có:
\(AD = {{DE} \over {\sin \widehat A}} = {{{{5\sqrt 3 } \over 2}} \over {\sin 40^\circ }} \approx 6,736\left( {cm} \right)\)
b) Trong tam giác vuông ADE, ta có:
Advertisements (Quảng cáo)
\(AE = AD.\cot g\widehat A \approx 6,736.\cot g40^\circ = 5,16\left( {cm} \right)\)
Ta có: \(AB = AE – BE = 5,16 – 2,5 = 2,66\left( {cm} \right)\)
Câu 62: Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat B,\widehat C\)


Theo hệ thức liên hệ giữa đường có và hình chiếu, ta có:
\(A{H^2} = HB.HC\)
Suy ra:
\(AH = \sqrt {HB.HC} = \sqrt {25.64} = \sqrt {1600} = 40\) (cm)
Trong tam giác vuông ABH, ta có:
\(tgB = {{AH} \over {HB}} = {{40} \over {25}} = 1,6\)
Suy ra:
\(\widehat B \approx 57^\circ 59’\)
Vì tam giác ABC vuông nên \(\widehat B + \widehat C = 90^\circ \)
Suy ra:
\(\widehat C = 90^\circ – \widehat B = 90^\circ – 57^\circ 59′ = 32^\circ 1’\)
Câu 63: Cho tam giác ABC có BC = 12cm, \(\widehat B = 60^\circ ,\widehat C = 40^\circ .\) Tính
a) Đường cao CH và cạnh AC;
b) Diện tích tam giác ABC.

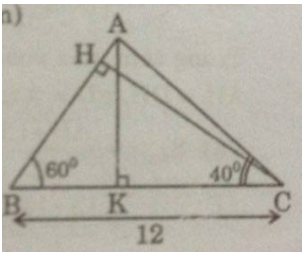
a) Trong tam giác vuông BCH, ta có:
\(CH = BC.\sin \widehat B = 12.\sin 60^\circ \approx 10,392\) (cm)
Trong tam giác vuông ABC, ta có:
\(\widehat A = 180^\circ – (60^\circ + 40^\circ ) = 80^\circ \)
Trong tam giác vuông ACH, ta có:
\(AC = {{CH} \over {\sin \widehat A}} \approx {{10,392} \over {\sin 80^\circ }} = 10,552\) (cm)
b) Kẻ \(AK \bot BC\)
Trong tam giác vuông ACK, ta có:
\(AK = AC.\sin \widehat C \approx 10,552.\sin 40^\circ = 6,783\) (cm)
Vậy \({S_{ABC}} = {1 \over 2}.AK.BC \approx {1 \over 2}.6,783.12 = 40,696\) (cm2)

