Câu 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 2.10, 2.11
Xét hình bs. 4. Tìm đẳng thức đúng
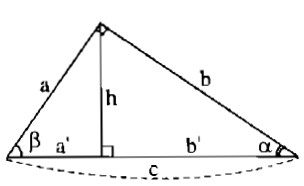
Câu 2.1:
(A) \(\sin \alpha = {a \over b}\); (B) \(sin\alpha = {b \over c}\);
(C) \(\sin \alpha = {{b’} \over b}\); (D) \(\sin \alpha = {h \over a}.\)
Câu 2.2:
(A) \(cos\alpha = {a \over b};\) (B) \(cos\alpha = {a \over c}\);
(C) \(cos\alpha = {b \over c}\); (D) \(cos\alpha = {b \over {b’}}.\)
Câu 2.3:
(A) \(tg\alpha = {b \over a}\); (B) \(tg\alpha = {b \over c}\) ;
(C) \(tg\alpha = {b \over h}\); (D) \(tg\alpha = {h \over {b’}}\).
Câu 2.4:
(A) \(\cot g\alpha = {b \over a}\); (B) \(\cot g\alpha = {b \over c}\);
Advertisements (Quảng cáo)
(C) \(\cot g\alpha = {a \over c}\); (D) \(\cot g\alpha = {h \over b}.\)
Câu 2.5:
(A) \(\sin \alpha = \sin \beta \); (B) \(\sin \alpha = \cos \beta\);
(C) \(\sin \alpha = tg\beta \); (D) \(\sin \alpha = {\mathop{\rm cotg}\nolimits} \beta \).
Câu 2.6:
(A) \(\cos \alpha = \cos \beta \); (B) \(\cos \alpha = tg\beta \);
(C) \(\cos \alpha = {\mathop{\rm cotg}\nolimits} \beta \); (D) \(\cos \alpha = \sin \beta \).
Câu 2.7:
Advertisements (Quảng cáo)
(A) \(tg\alpha = tg\beta \); (B) \(tg\alpha = cotg\beta \);
(C) \(tg\alpha = \sin \beta \); (D) \(tg\alpha = \cos \beta \).
Câu 2.8:
(A) \(\cot g\alpha = tg\beta \); (B) \(\cot g\alpha = cotg\beta \);
(C) \(\cot g\alpha = \cos \beta \); (D) \(\cot g\alpha = \sin \beta \).
Câu 2.9:
(A) cos2∝ + sin2β = 1 ; (B) sin2∝ + cos2β = 1 ;
(C)sin2∝ + cos2= 1 ; (D) cos2∝ + cos2β = 2.
Câu 2.10:
(A) tg∝ = sin∝ + cos∝ ; (B) tg∝ = sin∝ – cos∝ ;
(C) tg∝ = sin∝ .cos∝ ; (D) tg∝ = \({{\sin \alpha } \over {\cos \alpha }}.\)
Câu 2.11:
(A) cotg∝ = 1 + tg∝ ; (B) cotg∝ = 1 − tg∝ ;
(C)cotg∝ = 1.tg∝ ; (D) cotg∝ = \({1 \over {tg\alpha }}.\)

| 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2.10 | 2.11 |
| D | C | D | A | B | D | B | A | C | D |
D
|

