Bài 1: Cho ba điểm \(A, B, C\) cùng thuộc một mặt cầu và cho biết \(\widehat {ACB} = 90^0\). Trong các khẳng định sau khẳng định nào đúng?
a) Đường tròn qua ba điểm \(A, B, C\) nằm trên mặt cầu.
b) \(AB\) là một đường kính của mặt cầu đã cho.
c) \(AB\) không phải là đường kính của mặt cầu.
d) \(AB\) là đường kính của đường tròn giao tuyến tạo bởi mặt cầu và mặt phẳng \((ABC)\)
Ta có: Câu a) đúng vì mặt cầu giao với mặt phẳng \((ABC)\) theo một đường tròn.
Câu d) đúng vì trong đường tròn giao tuyến của mặt phẳng \((ABC)\) với mặt cầu, với giả thiết \(\widehat {ACB} = 90^0\). Suy ra \(AB\) là đường kính của đường tròn giao tuyến.
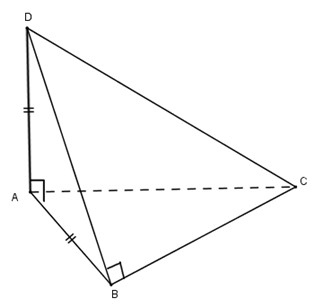
Bài 2: Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \((ABC)\) và cạnh \(BD\) vuông góc với cạnh \(BC\). Biết \(AB = AD = a\), tính diện tích xung quanh và thể tích của khối nón được tạo thành khi quay đường gấp khúc \(BDA\) quanh cạnh \(AB\).
Advertisements (Quảng cáo)
Vì \(∆ABD\) vuông góc tại \(A\), nên khi quay \(BDA\) quanh \(AB\) ta được hình nón tròn xoay đường cao \(AB = a\) và bán kính đáy bằng \(AD = r =a\).
Vậy \(V\)nón = \({1 \over 3}\pi {r^2}h = {1 \over 3}\pi {a^3}\)
\(S\)xq = \(πrl\) ở đó đường sinh \(l = a\sqrt2\) nên \(S\)xq = \(\sqrt2πa^2\).
Bài 3: Chứng minh rằng hình chóp có tất cả các cạnh bên bằng nhau nội tiếp được trong một mặt cầu.
Giả sử ta có hình chóp \(S.ABCD\), có các cạnh bên \(SA = SB = SC = SD = …\), kẻ \(SH \bot (ABCD)\), ta chứng minh được \(△SHA = △SHB = △SHC = △SHD = △…\) suy ra \(HA = HB = HC = HD = …\) \( \Rightarrow \) Đáy \(ABCD\)…, của hình chóp nội tiếp trong một đường tròn và chân \(H\) của đường cao \(SH\) là tâm đường tròn ngoại tiếp đa giác đáy. Dễ thấy, mọi điểm nằm trên đường cao \(SH\) đều cách đều các đỉnh \(A, B, C, D\) của đáy. Trong tam giác \(SAH\) chẳng hạn, ta kẻ đường trung trực của cạnh \(SA\), đường này cắt \(SH\) ở điểm \(I\). Dễ thấy: \(IS = IA = IB = IC = ID = …\) hay điểm \(I\) cách đều các đỉnh của hình chóp và do đó \(I\) là tâm mặt cầu đi qua các đỉnh của hình chóp.
Bài 4: Hình chóp \(S.ABC\) có một mặt cầu tiếp xúc với các cạnh \(SA, SB, SC\) và tiếp xúc với ba cạnh \(AB, BC, CA\) tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.
Advertisements (Quảng cáo)
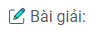
Gọi \(M, N, P\) theo thứ tự là các tiếp điểm của mặt cầu với các cạnh \(SA, SB, SC\); \(D, E, F\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CA\), các điểm \(D, E, F\) đồng thời cũng là tiếp điểm của mặt cầu với các cạnh \(AB, BC, CA\).
Ta có: \(AD = AF \Rightarrow AB = AC\)
\(BD = BE \Rightarrow BC = AB\)
\( \Rightarrow AB = BC = CA\)
\( \Rightarrow △ABC\) là tam giác đều… (1)
Ta lại có \(AM = AD; BN = BD = AD\)
và \(SM = SN = SP\)
\( \Rightarrow SM + AM = SN + NB\)
\( \Rightarrow SA = SB\)
Chứng minh tương tự ta có: \(SA = SB = SC\).
Gọi \(H\) là chân đường cao của hình chóp kẻ từ đỉnh \(S\), ta có:
\(△SHA = △SHB =△SHC\)\( \Rightarrow HA = HB = HC\)
\( \Rightarrow H\) là tâm của tam giác đều \(ABC\) (2)
Từ (1) và (2) suy ra hình chóp \(S.ABC\) là hình chóp tam giác đều.

