Bài 17: Dùng phương pháp đổi biến số tính các tích phân sau:
a) \(\int\limits_0^1 {\sqrt {x + 1} dx;} \) b) \(\int\limits_0^{{\pi \over 4}} {{{\tan x} \over {{{\cos }^2}x}}} dx;\)
c) \(\int\limits_0^1 {{t^3}} {\left( {1 + {t^4}} \right)^3}dt;\) d) \(\int\limits_0^1 {{{5x} \over {{{\left( {{x^2} + 4} \right)}^2}}}} dx;\)
e) \(\int\limits_0^{\sqrt 3 } {{{4x} \over {\sqrt {{x^2} + 1} }}} dx;\) f) \(\int\limits_0^{{\pi \over 6}} {\left( {1 – \cos 3x} \right)} \sin 3xdx.\)
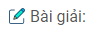
a) Đặt \(u = \sqrt {x + 1} \Rightarrow {u^2} = x + 1 \Rightarrow 2udu = dx.\)
Đổi cận
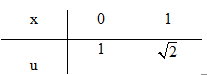
\(\int\limits_0^1 {\sqrt {x + 1} } dx = \int\limits_1^{\sqrt 2 } {u.2udu = 2\int\limits_1^{\sqrt 2 } {{u^2}du} } \)
\(= \left. {2.{{{u^3}} \over 3}} \right|_1^{\sqrt 2 } = {2 \over 3}\left( {2\sqrt 2 – 1} \right)\)
b) Đặt \(u = \tan x \Rightarrow du = {{dx} \over {{{\cos }^2}x}}\)
\(\int\limits_0^{{\pi \over 4}} {{{\tan x} \over {{{\cos }^2}x}}} dx = \int\limits_0^1 {udu = } \left. {{{{u^2}} \over 2}} \right|_0^1 = {1 \over 2}\)
c) Đặt \(u = 1 + {t^4} \Rightarrow du = 4{t^3}dt \Rightarrow {t^3}dt = {{du} \over 4}\)

\(\int\limits_0^1 {{t^3}\left( {1 + {t^4}} \right)} dt = {1 \over 4}\int\limits_1^2 {{u^3}} du = \left. {{1 \over 4}{{{u^4}} \over 4}} \right|_1^2 = {1 \over {16}}\left( {16 – 1} \right) \)
\(= {{15} \over {16}}\)
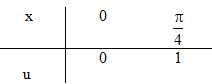
d) Đặt \(u = {x^2} + 4 \Rightarrow du = 2xdx \Rightarrow xdx = {1 \over 2}du\)
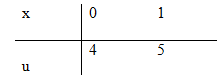
\(\int\limits_0^1 {{{5x} \over {{{\left( {{x^2} + 4} \right)}^2}}}} dx = {5 \over 2}\int\limits_4^5 {{{du} \over {{u^2}}}} = \left. {{5 \over 2}\left( { – {1 \over u}} \right)} \right|_4^5 = {1 \over 8}\)
Advertisements (Quảng cáo)
e) Đặt \(u = \sqrt {{x^2} + 1} \Rightarrow {u^2} = {x^2} + 1 \Rightarrow udu = xdx\)
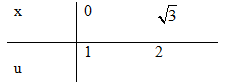
\(\int\limits_0^{\sqrt 3 } {{{4x} \over {\sqrt {{x^2} + 1} }}} dx = 4\int\limits_1^2 {{{udu} \over u}} = \left. {4u} \right|_1^2 = 4\)
f) Đặt \(u = 1 – \cos 3x \Rightarrow du = 3\sin 3xdx \)
\(\Rightarrow \sin 3xdx = {1 \over 3}du\)
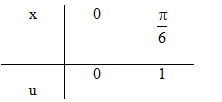
\(\int\limits_0^{{\pi \over 6}} {\left( {1 – \cos 3x} \right)} \sin 3xdx = {1 \over 3}\int\limits_0^1 {udu = \left. {{{{u^2}} \over 6}} \right|} _0^1 = {1 \over 6}\)
Bài 18: Dùng phương pháp tích phân từng phần để tính các tích phân sau:
a) \(\int\limits_1^2 {{x^5}} \ln xdx;\) b) \(\int\limits_0^1 {\left( {x + 1} \right)} {e^x}dx;\)
c) \(\int\limits_0^\pi {{e^x}} \cos xdx;\) d) \(\int\limits_0^{{\pi \over 2}} {x\cos xdx.} \)
a) Đặt
Advertisements (Quảng cáo)
\(\left\{ \matrix{
u = \ln x \hfill \cr
dv = {x^5}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {{dx} \over x} \hfill \cr
v = {{{x^6}} \over 6} \hfill \cr} \right.\)
\(\int\limits_1^2 {{x^5}} \ln xdx = \left. {{{{x^6}} \over 6}\ln x} \right|_1^2 – {1 \over 6}\int\limits_1^2 {{x^5}} dx \)
\(= \left. {\left( {{{{x^6}} \over 6}\ln x – {{{x^6}} \over {36}}} \right)} \right|_1^2 = {{32} \over 3}\ln 2 – {7 \over 4}\)
b) Đặt
\(\left\{ \matrix{
u = x + 1 \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
\(\int\limits_0^1 {\left( {x + 1} \right)} {e^x}dx = \left. {\left( {x + 1} \right){e^x}} \right|_0^1 – \int\limits_0^1 {{e^x}dx = e} \)
c) Đặt \(I = \int\limits_0^\pi {{e^x}\cos xdx} \)
Đặt
\(\left\{ \matrix{
u = {e^x} \hfill \cr
dv = \cos xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {e^x}dx \hfill \cr
v = {\mathop{\rm s}\nolimits} {\rm{inx}} \hfill \cr} \right.\)
Suy ra \(I = \left. {{e^x}{\mathop{\rm s}\nolimits} {\rm{inx}}} \right|_0^\pi – \int\limits_0^\pi {{e^x}\sin {\rm{x}}dx} = – \int\limits_0^\pi {{e^x}\sin {\rm{x}}dx} \)
Đặt
\(\left\{ \matrix{
u = {e^x} \hfill \cr
dv = \sin {\rm{x}}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {e^x}dx \hfill \cr
v = – \cos x \hfill \cr} \right.\)
Do đó \(I = – \left[ {\left. {\left( { – {e^x}\cos x} \right)} \right|_0^\pi + \int\limits_0^\pi {{e^x}\cos xdx} } \right] \)
\(= {e^\pi }\cos \pi – {e^0}.\cos 0 – I\)
\( \Rightarrow 2I = – {e^\pi } – 1 \Rightarrow I = – {1 \over 2}\left( {{e^\pi } + 1} \right)\)
d) Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \cos xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {\mathop{\rm s}\nolimits} {\rm{inx}} \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {x\cos xdx = \left. {x\sin x} \right|_0^{{\pi \over 2}}} – \int\limits_0^{{\pi \over 2}} {\sin {\rm{x}}dx} \)
\(= \left. {\left( {x\sin x + \cos x} \right)} \right|_0^{{\pi \over 2}} = {\pi \over 2} – 1\)
Bài 19: Tính
a) \(\int\limits_0^1 {\sqrt {{t^5} + 2t} } \left( {2 + 5{t^4}} \right)dt;\)
b) \(\int\limits_0^{{\pi \over 2}} {x\sin {\rm{xcosx}}dx} .\)
giải
a) Đặt \(u = \sqrt {{t^5} + 2t} \Rightarrow {u^2} = {t^5} + 2t \)
\(\Rightarrow 2udu = \left( {5{t^4} + 2} \right)dt\)
|
t |
0 |
1 |
|
u |
0 |
\(\sqrt 3 \) |
\(\int\limits_0^1 {\sqrt {{t^5} + 2t} } \left( {2 + 5{t^4}} \right)dt = \int\limits_0^{\sqrt 3 } {2{u^2}du = \left. {{{2{u^3}} \over 3}} \right|} _0^{\sqrt 3 } = 2\sqrt 3 \)
b) Ta có \(I = \int\limits_0^{{\pi \over 2}} {x\sin x\cos xdx = {1 \over 2}} \int\limits_0^{{\pi \over 2}} {x\sin 2xdx} \)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \sin 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = – {1 \over 2}\cos 2x \hfill \cr} \right.\)
Do đó \(I = \left. {{1 \over 2}\left( { – {1 \over 2}x\cos x2x} \right)} \right|_0^{{\pi \over 2}} + {1 \over 4}\int\limits_0^{{\pi \over 2}} {\cos 2xdx}\)
\(= {\pi \over 8} + \left. {{1 \over 8}\sin 2x} \right|_0^{{\pi \over 2}} = {\pi \over 8}\)

