Bài 15: Cho tam giác \(ABC\) cố định và một điểm \(S\) thay đổi. Thể tích của khối chóp \(S.ABC\) có thay đổi hay không nếu:
a) Đỉnh \(S\) di chuyển trên một mặt phẳng song song với mặt phẳng \((ABC)\) ;
b) Đỉnh \(S\) di chuyển trên một mặt phẳng song song với chỉ một cạnh đáy ;
c) Đỉnh \(S\) di chuyển trên một đường thẳng song song với một cạnh đáy ?
a) Thể tích khối chóp \(S.ABC\) không đổi do diện tích đáy và chiều cao không đổi.
b) Có thể thay đổi do chiều cao thay đổi.
c) Không đổi do diện tích đáy và chiều cao không đổi.
Bài 16: Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối tứ diện này bằng một số \(k>0\) cho trước.
Advertisements (Quảng cáo)

Cho khối tứ diện \(ABCD\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(MB = kMC\), khi đó \({S_{BMD}} = k{S_{CMD}} \Rightarrow {V_{ABMD}} = k{V_{AMCD}}\)
Mặt phẳng \((AMD)\) chia khối tứ diện \(ABCD\) thành hai khối tứ diện có tỉ số thể tích bằng \(k\).
Bài 17: Tính thể tích của khối hộp \(ABCD.A’B’C’D’\), biết rằng \(AA’B’D’\) là khối tứ diện đều cạnh \(a\).
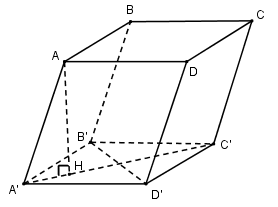
\(AA’B’D’\) là tứ diện đều nên đường cao \(AH\) có \(H\) là tâm của tam giác đều \(A’B’D’\) cạnh \(a\) do đó”
\(\eqalign{
& A’H = {2 \over 3}A’O’ = {2 \over 3}{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 3} \cr
& \Rightarrow A{H^2} = AA{‘^2} – A'{H^2} = {a^2} – {{{a^2}} \over 3} = {{2{a^2}} \over 3} \cr
& \Rightarrow AH = a\sqrt {{2 \over 3}} = {{a\sqrt 6 } \over 3} \cr} \)
Advertisements (Quảng cáo)
Diện tích tam giác đều \(A’B’D’\): \({S_{A’B’D’}} = {{{a^2}\sqrt 3 } \over 4}\)
Diện tích hình thoi \(A’B’C’D’\): \({S_{A’B’C’D’}} = 2{S_{B’C’D’}} = {{{a^2}\sqrt 3 } \over 2}\)
Vậy thể tích khối hộp đã cho là \(V = B.h = {{{a^2}\sqrt 3 } \over 2}.{{a\sqrt 6 } \over 3} = {{{a^3}\sqrt 2 } \over 2}\)
Bài 18: Tính thể tích của khối lăng trụ \(n\)-giác đều có tất cả các cạnh đều bằng \(a\).

Gọi \({A_1}{A_2}…{A_n}\) là đáy của khối lăng trụ \(n\)-giác đều và \(O\) là tâm của đáy.
Gọi \(I\) là trung điểm của \({A_1}{A_2}\) ta có \(OI \bot {A_1}{A_2}\).
Trong \(\Delta {A_1}IO\): \(\cot \widehat {{A_1}IO} = {{OI} \over {{A_1}I}} \Rightarrow OI = {a \over 2}\cot {\pi \over n}\).
Diện tích đáy của khối lăng trụ đều là \(S = n.{S_{O{A_1}{A_2}}} = n{1 \over 2}a.{a \over 2}\cot {\pi \over n} = {1 \over 4}n{a^2}\cot {\pi \over n}\)
Chiều cao của khối lăng trụ đều là \(a\) nên thể tích của nó là:\(V = B.h = {1 \over 4}n{a^3}.\cot {\pi \over n}\)
Bài 19: Cho khối lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác \(ABC\) vuông tại \(A, AC = b\). \(\widehat {ACB} = {60^0}\). Đường thẳng \(BC’\) tạo với mp \((AA’C’C)\) một góc \({30^0}\).
a) Tính độ dài đoạn thẳng \(AC\).
b) Tính thể tích khối lăng trụ đã cho.
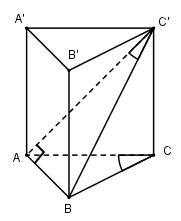
a) Ta có: \(BA \bot AC\) và \(BA \bot AA’\) nên \(BA \bot \left( {ACC’A’} \right)\)
Vậy \(AC’\) là hình chiếu của \(BC’\) trên mp \((ACC’A’)\) nên \(\widehat {AC’B} = {30^0}\)
Trong tam giác vuông \(BAC’\), ta có:
\(\cot {30^0} = {{AC’} \over {AB}}\)
\(\Rightarrow AC’ = AB.cot{30^0} = AC.\tan {60^0}.\cot {30^0} \)
\(= b\sqrt 3 .\sqrt 3 = 3b\)
b) Trong tam giác vuông \(ACC’\), ta có: \(CC{‘^2} = AC{‘^2} – A{C^2} = 9{b^2} – {b^2} = 8{b^2} \)
\(\Rightarrow CC’ = 2\sqrt 2 b\)
Diện tích là: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}b\sqrt 3 .b = {{{b^2}\sqrt 3 } \over 2}\)
Thể tích khối lăng trụ \(V = S.h = {{{b^2}\sqrt 3 } \over 2}.2\sqrt 2 b = {b^3}\sqrt 6 \)

