CÂU HỎI TRẮC NGHIỆM:
Bài 1: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất
(A) Năm cạnh (B) Bốn cạnh
(C) Ba cạnh (D) Hai cạnh.
Chọn C
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất 3 cạnh
Bài 2: Cho khối chóp có đáy là \(n\)-giác. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
(A) Số cạnh của khối chóp bằng \(n + 1\) ;
(B) Số mặt của khối chóp bằng \(2n\) ;
(C) Số đỉnh của khối chóp bằng \(2n + 1\) ;
(D) Số mặt của khối chóp bằng số đỉnh của nó.
Chọn D
Số mặt của khối chóp bằng số đỉnh của nó.
Bài 3: Phép đối xứng qua mp \((P) \) biến đường thẳng \(d\) thành chính nó khi và chỉ khi:
(A) \(d\) song song với \((P)\)
(B). \(d\) nằm trên \((P)\)
(C) \(d \bot \left( P \right)\)
(D). \(d\) nằm trên \((P)\) hoặc \(d \bot \left( P \right)\)
Chọn D
Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành chính nó khi và chỉ khi d nằm trên (P) hoặc \(d \bot \left( P \right)\).
Bài 4: Cho hai đường thẳng \(d\) và \(d’\) cắt nhau. Có bao nhiêu phép đối xứng qua mặt phẳng biến \(d\) thành \(d’\)?
(A) Có một (B) Có hai
(C) Không có (D) Có vô số
Chọn B
Có hai phép đối xứng qua mặt phẳng biến \(d\) thành \(d’\).
Bài 5: Có hai đường thẳng phân biệt \(d\) và \(d’\) đồng phẳng. Có bao nhiêu phép đối xứng qua mặt phẳng biến \(d\) thành \(d’\)?
(A) Không có (B) Có một
(C) Có hai (D) Có một hoặc hai
Chọn D
Bài 6: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
(A) Một (B) Hai (C) Ba (D) Bốn
Chọn D
Hình chóp tứ giác đều \(S.ABCD\) có \(4\) mặt phẳng đối xứng là: mp \((SAC)\), mp \((SBD)\), mp trung trực của đoạn \(AB\) và mặt phẳng trung trực của đoạn \(AD\). Chọn D.

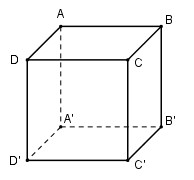
Bài 7: Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?
(A) Một (B) Hai (C) Ba (D) Bốn
Hình hộp đứng \(ABCD.A’B’C’D’\) có đáy là hình thoi (không là hình vuông) có 3 mặt phẳng đối xứng, đó là ba mặt phẳng trung trực của ba cạnh \(AB, AD, AA’\). Chọn C.
Bài 8. Cho phép vị tự tâm \(O\) biến điểm \(A\) thành điểm \(B\), biết rằng \(OA=2OB\). Khi đó tỉ số phép vị tự là bao nhiêu?
(A) \(2\) (B) \(– 2\) (C) \( \pm {1 \over 2}\) (D) \({1 \over 2}\)
Giả sử \({V_k}:A \to B\) thì \(\overrightarrow {OB} = k\overrightarrow {OA} \Rightarrow OB = \left| k \right|OA \Rightarrow \left| k \right| = {1 \over 2} \Rightarrow k = \pm {1 \over 2}\). Chọn C.
Bài 9: Cho hai đường thẳng song song \(d\) và \(d’\) và một điểm \(O\) không nằm trên chúng. Có bao nhiêu phép vị tự tâm \(O\) biến \(d\) thành \(d’\)?
(A) Có một (B) Không có
(C) Có hai (D) Có một hoặc không có.
Chọn D.
Bài 10. Khối tám mặt đều thuộc loại:
(A) \(\left\{ {3;3} \right\}\) (B) \(\left\{ {4;3} \right\}\)
(C) \(\left\{ {5;3} \right\}\) (D) \(\left\{ {3;3} \right\}\)
Chọn D.
Bài 11: Khối hai mươi mặt đều thuộc loại:
(A) \(\left\{ {3;4} \right\}\) (B) \(\left\{ {3;5} \right\}\)
(C) \(\left\{ {4;3} \right\}\) (D) \(\left\{ {4;5} \right\}\)
Chọn B
Bài 12: Nếu ba kích thước của một khối hộp chữ nhật tăng lên \(k\) lần thì thể tích của nó tăng lên:
(A) \(k\) lần (B) \({k^2}\) lần
(C) \({k^3}\) lần (D) \(3{k^3}\) lần
\(a’ = ka,b’ = kb,c’ = kc\)
\(V’ = a’b’c’ = {k^3}abc = {k^3}V\). Chọn C.
Bài 13: Tổng diện tích các mặt của một hình lập phương bằng \(96\). Thể tích của khối lập phương đó là:
(A) \(64\) (B) \(91\) (C) \(84\) (D) \(48\)
Tổng diện tích các mặt của hình lập phương cạnh a bằng \(6{a^2} = 96 \Rightarrow a = 4\)
Thể tích khối lập phương đó là \(V = {a^3} = 64\). Chọn A.
Bài 14: Ba kích thước của một khối hộp chữ nhật làm thành một cấp số nhân có công bội là \(2\). Thể tích hình hộp đã cho là \(1728\). Khi đó các kích thước của hình hộp là:
Advertisements (Quảng cáo)
(A) \(8, 16, 32\) (B) \(2, 4, 8\)
(C) \(2\sqrt 3 ,4\sqrt 3 ,38\) (D) \(6, 12, 24\)
Ba kích thước của hình hộp chữ nhật là \(a,2a,4a\)
Thể tích hình hộp là: \(V = a.2a.4a = 8{a^3} = 1728 \Leftrightarrow a = 6\). Chọn D.
Bài 15: Các đường chéo của các mặt của hình hộp chữ nhật bằng \(\sqrt 5 ,\sqrt {10} ,\sqrt {13} \). Thể tích của hình hộp đó là:
(A) \(4\) (B) \(5\) (C) \(6\) (D) \(12\)
Gọi kích thước của hình hộp chữ nhật là a, b, c.
Ta có:
\(\eqalign{
& {a^2} + {b^2} = 5,{b^2} + {c^2} = 10,{c^2} + {a^2} = 13\cr& \Rightarrow {a^2} + {b^2} + {c^2} = {1 \over 2}\left( {5 + 10 + 13} \right) = 14 \cr
& \Rightarrow {a^2} = 4,{b^2} = 1,{c^2} = 9 \Rightarrow a = 2,b = 1,c = 3 \cr
& \Rightarrow V = abc = 2.1.3 = 6 \cr} \)
Chọn C.
Bài 16: Một khối lăng trụ đứng tam giác có cạnh đáy bằng \(37, 13, 30\) và diện tích xung quanh bằng \(480\). Khi đó thể tích của khối lăng trụ là:
(A) \(2010\) (B) \(1010\)
(C) \(1080\) (D) \(2040\)
Chu vi đáy: \(C = 80\)
Diện tích đáy: \(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = 180\)
Diện tích xung quanh \({S_{xq}} = C.h = 480\)
Chiều cao lăng trụ \(h = {{480} \over {80}} = 6\)
Thể tích của khối lăng trụ \(V = S.h = 180.6 = 1080\)
Chọn C.
Bài 17: Một khối lăng trụ tam giác có các cạnh đáy bằng \(13, 14, 15\), cạnh bên tạo với mặt phẳng đáy một góc \({30^0}\) và có chiều dài bằng \(8\). Khi đó thể tích của khối lăng trụ là:
(A) \(340\) (B) \(336\)
(C) \(274\sqrt 3 \) (D) \(124\sqrt 3 \)
Gọi H là hình chiếu của A trên mp(A’B’C’)
Ta có: \(\widehat {AA’H} = {30^0}\,\,;\,\,AA’ = 8\,\,;\,\,AH = AA\sin {30^0} = 4\)
Diện tích đáy \({S_{A’B’C’}} = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = 84\)
Thể tích khối lăng trụ là: \(V = S.h = 84.4 = 336\)
Chọn B.

Bài 18: Đáy của một hình hộp đứng là hình thoi cạnh \(a\), góc nhọn \({60^0}\). Đường chéo lớn của đáy bằng đường chéo nhỏ của hình hộp. Khi đó thể tích của hình hộp là:
(A) \({a^3}\) (B) \({a^3}\sqrt 3 \)
(C) \({{{a^3}\sqrt 3 } \over 2}\) (D) \({{{a^3}\sqrt 3 } \over 6}\)
Giải

Tam giác A’B’C’ là tam giác đều cạnh a
Ta có:
\(\eqalign{
& A’C’ = a,B’D’ = 2B’O’ = a\sqrt 3 = A’C \cr
& \Rightarrow CC’ = \sqrt {A'{C^2} – A’C{‘^2}} = \sqrt {3{a^2} – {a^2}} = a\sqrt 2 \cr} \)
Diện tích đáy \({S_{A’B’C’D’}} = {1 \over 2}A’C’.B’D’ = {{{a^2}\sqrt 3 } \over 2}\)
Thể tích khối hộp: \(V = S.h = {{{a^2}\sqrt 3 } \over 2}.a\sqrt 2 = {{{a^3}\sqrt 6 } \over 2}\)
Chọn D.
Bài 19: Khi độ dài cạnh của hình lập phương tăng thêm \(2cm\) thì thể tích của nó tăng thêm \(98c{m^3}\). Cạnh của hình lâp phương đã cho là:
(A) \(4cm\) (B) \(5cm\)
(C) \(6cm\) (D) \(3cm\)
Advertisements (Quảng cáo)
Giải
Gọi \(a\) là độ dài cạnh hình lập phương.
Ta có phương trình \({\left( {a + 2} \right)^3} – {a^3} = 98 \Leftrightarrow 3{a^2} + 6a – 45 = 0 \Leftrightarrow a = 3\)
Chọn D.
Bài 20: Cho một hình hộp với sáu mặt đều là hình thoi cạnh \(a\), góc nhọn bằng \({60^0}\). Khi đó thể tích của hình hộp là:
(A) \({{{a^3}\sqrt 3 } \over 3}\) (B) \({{{a^3}\sqrt 2 } \over 2}\)
(C) \({{{a^3}\sqrt 2 } \over 3}\) (D) \({{{a^3}\sqrt 3 } \over 2}\)

Giải
\(\Delta A’B’C’\) đều cạnh a
\(A’C’ = a\,\,;\,\,B’D’ = 2B’O’ = a\sqrt 3 \)
Tương tự \(BA’ = BC’ = BB’ = a\) nên hình chiếu \(H\) của \(B\) trên mp(A’B’C’D’) là tâm của tam giác đều \(A’B’C’\)
Ta có: \(BH = \sqrt {BB{‘^2} – B'{H^2}} = \sqrt {{a^2} – {{{a^2}} \over 3}} = {{a\sqrt 6 } \over 3}\)
\({S_{A’B’C’D’}} = {1 \over 2}A’C’.B’D’ = {1 \over 2}a.a\sqrt 3 = {{{a^2}\sqrt 3 } \over 2}\)
Thể tích khối hộp là: \(V = B.h = {{{a^2}\sqrt 3 } \over 2}.{{a\sqrt 6 } \over 3} = {{{a^3}\sqrt 2 } \over 2}\) Chọn B.
Bài 21: Cho một hình lập phương có cạnh bằng \(a\). Khi đó thể tích của khối tám mặt đều mà các đỉnh là tâm của các mặt của hình lập phương đã cho bằng:
(A) \({{{a^3}\sqrt 3 } \over 2}\) (B) \({{{a^3}\sqrt 2 } \over 9}\)
(C) \({{{a^3}} \over 3}\) (D) \({{{a^3}} \over 6}\)
Ta có khối tám mặt đều có cạnh bằng \({{a\sqrt 2 } \over 2}\) ( theo bài 14 trang 20)
Thể tích khối tám mặt đều là \(V = 2{V_{M.PQRS}} = 2.{1 \over 3}.{a \over 2}{\left( {{{a\sqrt 2 } \over 2}} \right)^2} = {{{a^3}} \over 6}\)
Chọn D.
Bài 22: Cho khối tứ diện đều có cạnh bằng \(a\). Khi đó, thể tích của khối tám mặt đều mà các đỉnh là trung điểm của các cạnh của khối tứ diện đã cho là:
(A) \({{{a^3}\sqrt 2 } \over {24}}\) (B) \({{{a^3}\sqrt 3 } \over {12}}\)
(C) \({{{a^3}\sqrt 2 } \over 6}\) (D) \({{{a^3}\sqrt 3 } \over {24}}\)

Khối tám mặt đều đã cho có cạnh là \({a \over 2}\) và \(RS = MP = {{a\sqrt 2 } \over 2}\)
Thể tích khối tám mặt đều là \(V = 2.{V_{R.MNPQ}}\)
\(= 2.{1 \over 3}.{{RS} \over 2}.{S_{MNPQ}} = 2.{1 \over 3}.{{a\sqrt 2 } \over 4}.{{{a^2}} \over 4} = {{{a^3}\sqrt 2 } \over {24}}\)
Chọn A
Bài 23: Cho khối \(12\) mặt đều \((H)\) có thể tích \(V\) và diện tích mỗi mặt của nó bằng . Khi đó tổng các khoảng cách từ một điểm nằm trong \((H)\) đến các mặt của nó bằng:
(A) \({{3V} \over {4S}}\) (B) \({V \over {4S}}\)
(C) \({{3V} \over S}\) (D) \({V \over {12S}}\)
Giải
Gọi \({h_1},{h_2},…,{h_{12}}\) là khoảng cách từ M nằm trong (H) đến các mặt của khối 12 mặt đều
Ta có: \(V = {1 \over 2}{h_1}S + {1 \over 3}{h_2}S + … + {1 \over 3}{h_{12}}S\)
\(= {1 \over 3}S\left( {{h_1} + {h_2} + … + {h_{12}}} \right)\)
Suy ra \({h_1} + {h_2} + … + {h_{12}} = {{3V} \over S}\)
Chọn C.
Bài 24: Một khối lăng trụ tam giác có các cạnh đáy bằng \(19, 20, 37\), chiều cao của khối lăng trụ bằng trung bình cộng của các cạnh đáy. Khi đó thể tích của khối lăng trụ là:
(A) \(2888\) (B) \(1245\sqrt 2 \) (C) \(1123\) (D) \(4273\)
Giải
Chiều cao của lăng trụ bằng: \(h = {1 \over 3}\left( {19 + 20 + 37} \right) = {{76} \over 3}\)
Diện tích đáy \(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = 114\)
Thể tích khối lăng trụ \(V = S.h = {{76} \over 3}.114 = 2888\)
Chọn A.
Bài 25: Đáy của một hình hộp là một hình thoi có cạnh bằng \(6cm\) và góc nhọn bằng \({45^0}\), cạnh bên của hình hộp dài \(10cm\) và tạo với mặt phẳng đáy một góc \({45^0}\). Khi đó thể tích của hình hộp là:
(A) \(124\sqrt 3 \,\,c{m^3}\) (B) \(180\,\,c{m^3}\)
(C) \(120\sqrt 2 \,\,c{m^3}\) (D) \(180\sqrt 2 \,\,c{m^3}\)

Gọi \(H\) là hình chiếu của \(B’\) trên mp \((ABCD)\)
\(B’H = BB’.\sin {45^0} = 10.{{\sqrt 2 } \over 2} = 5\sqrt 2 \)
Diện tích đáy \({S_{ABCD}} = 2{S_{ABC}} = {a^2}\sin {45^0} = {{{a^2}\sqrt 2 } \over 2} = 18\sqrt 2 \)
Thể tích hình hộp \({V_{ABCD}} = {S_{ABCD}}.B’H = 18\sqrt 2 .5\sqrt 2 = 180\)
Chọn B.
Bài 26: Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh \(12cm\) rồi gấp lại thành nột hình hộp chữ nhật không có nắp. Nếu dung tích của cái hộp đó là \(4800\) \(c{m^3}\) thì cạnh tấm bìa đó có độ dài là:
(A) \(42cm\) (B) \(36cm\)
(C) \(44cm\) (D) \(38cm\)

Gọi cạnh tấm bìa là \(x\) thì diện tích đáy hình hộp là \(S = {\left( {x – 24} \right)^2}\)
Thể tích hình hộp là \(V = S.h = 12{\left( {x – 24} \right)^2} = 4800 \Leftrightarrow x = 44\,\,cm\)
Chọn C.
Bài 27: Cho một hình chóp tam giác đều có cạnh đáy bằng \(a\) và cạnh bên tạo với mặt phẳng đáy một góc \(\alpha \). Thể tích của hình chóp đó là:
(A) \({{{a^3}\cot \alpha } \over {12}}\) (B) \({{{a^3}tan\alpha } \over {12}}\)
(C) \({{{a^2}tan\alpha } \over {12}}\) (D) \({{{a^3}tan\alpha } \over 4}\)

Gọi \(H\) là tâm của tam giác đều \(ABC\) thì \(SH \bot \left( {ABC} \right)\)
\(\tan \alpha = {{SH} \over {AH}} \Rightarrow SH = {{a\sqrt 3 } \over 3}\tan \alpha \)
Thể tích hình chóp là: \(V = {1 \over 3}{S_{ABC}}.SH = {1 \over 3}{{{a^2}\sqrt 3 } \over 4}{{a\sqrt 3 } \over 3}\tan \alpha = {{{a^3}\tan \alpha } \over {12}}\)
Chọn B.
Bài 28: Một hình chóp tam giác đều có cạnh bên bằng \(b\) và cạnh bên tạo với mặt phẳng đáy một góc \(\alpha \). Thể tích của hình chóp là:
(A) \({3 \over 4}{b^3}{\cos ^2}\alpha \sin \alpha \) (B) \({{\sqrt 3 } \over 4}{b^3}{\cos ^2}\alpha \sin \alpha \)
(C) \({3 \over 4}{b^3}\cos \alpha {\sin ^2}\alpha \) (D) \({{\sqrt 3 } \over 4}{b^3}\cos \alpha \sin \alpha \)

Gọi \(H\) là tâm của tam giác đều \(ABC\) cạnh \(a\).
\(SH \bot \left( {ABC} \right)\) và \(\widehat {SAH} = \alpha \). I là trung điểm của BC, \(AH = {2 \over 3}.{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 3}\)
Trong tam giác vuông AHS có \(\cos \alpha = {{AH} \over {SA}} \Rightarrow b\cos \alpha = {{a\sqrt 3 } \over 3} \Rightarrow a = b\sqrt 3 \cos \alpha \)
Diện tích tam giác ABC: \({S_{ABC}} = {{{a^2}\sqrt 3 } \over 4} = {{3\sqrt 3 } \over 4}{b^2}{\cos ^2}\alpha \)
Mặt khác \(SH = SA\sin \alpha = b\sin \alpha \)
Thể tích hình chóp là \(V = {1 \over 3}{S_{ABC}}.SH = {{\sqrt 3 } \over 4}{b^3}{\cos ^2}\alpha \sin \alpha \)
Chọn B.
Bài 29: Cho hình chóp tứ giác đêu \(H\) có diện tích đáy bằng \(4\) và diện tích của một mặt bên bằng \(\sqrt 2 \). Thể tích của \(H\) là:
(A) \({{4\sqrt 3 } \over 3}\) (B) \(4\) (C) \({4 \over 3}\) (D) \({{4\sqrt 3 } \over 2}\)
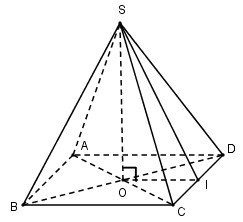
Gọi O là tâm hình vuông ABCD, I là trung điểm của CD
\(\eqalign{
& SO \bot \left( {ABCD} \right),{S_{ABCD}} = 4 = C{D^2} \Rightarrow CD = 2 \cr
& {S_{SCD}} = {1 \over 2}SI.CD = \sqrt 2 \Rightarrow SI = \sqrt 2 \cr
& S{O^2} = S{I^2} – O{I^2} = {\left( {\sqrt 2 } \right)^2} – {1^2} = 1 \Rightarrow SO = 1 \cr
& {V_H} = {1 \over 3}SO.{S_{ABCD}} = {4 \over 3} \cr} \)
Chọn C.
Bài 30: Một khối chóp tam giác có cạnh đáy bằn \(6, 8, 10\). Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:
(A) \(16\sqrt 3 \) (B) \(8\sqrt 3 \) (C) \(16{{\sqrt 2 } \over 3}\) (D) \(16\pi \)

Kẻ đường cao SH của hình chóp S.ABC
\(SH = SA.\sin {60^0} = 4.{{\sqrt 3 } \over 2} = 2\sqrt 3 \)
Diện tích tam giác ABC là \({S_{ABC}} = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = 24\)
Thể tích của khối chóp là \(V = {1 \over 3}{S_{ABC}}.SH = {1 \over 3}.24.2\sqrt 3 = 16\sqrt 3 \)
Chọn A.
Bài 31: Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên n lần thì thể tích của nó tăng lên:
(A) \({n^2}\) lần (B) \(2{n^2}\) lần
(C) \({n^3}\) lần (D) \(2{n^3}\) lần
Ta có \(V = B.h\). Nếu cạnh đáy của đa giác đều tăng lên n lần thì diện tích đáy tăng lên \({n^2}\) lần, khi đó thể tích tăng lên \({n^3}\) lần.
Chọn C.
Bài 32: Khi chiều cao của một hình chóp đều tăng lên n lần nhưng mỗi cạnh đáy giảm đi n lần thì thể tích của nó:
(A) Không thay đổi (B) Tăng lên n lần
(C) Tăng lên (n – 1) lần (D) Giảm đi n lần.
Ta có \(V = B.h\). Nếu cạnh đáy của đa giác đều giảm đi n lần thì diện tích đáy giảm đi \({n^2}\) lần, khi đó thể tích giảm n lần.
Chọn D.

