Bài 11: Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó.
Giải
a) Giả sử \({V_k}\) là phép vị tự tỉ số \(k\) biến đường thẳng \(a\) thành đường thẳng \(a’\), lấy \(M,N \in a\) và \({V_k}\left( M \right) = M’;{V_k}\left( N \right) = N’;M’,N’ \in a’\).
Ta có : \(\overrightarrow {M’N’} = k\overrightarrow {MN} \Rightarrow \overrightarrow {MN} \) cùng phương với \(\overrightarrow {M’N’} \) do đó hai đường thẳng \(a\) và \(a’\) song song hoặc trùng nhau.
b) Giả sử phép vị tự \({V_k}\) biến mặt phẳng \(\left( \alpha \right)\) thành mp \(\left( {\alpha ‘} \right)\). Lấy trên \(\left( \alpha \right)\) hai đường thẳng cắt nhau \(a\) và \(b\) thì ảnh của chúng qua \({V_k}\) là hai đường thẳng \(a’\) và \(b’\) nằm trên \(\left( {\alpha ‘} \right)\) và lần lượt song song hoặc trùng với \(a\) và \(b\). Từ đó suy ra hai mặt phẳng \(\left( \alpha \right)\) và \(\left( {\alpha ‘} \right)\) song song hoặc trùng nhau.
Bài 12: Cho một khối tứ diện đều. Hãy chứng minh rằng:
a) Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.
b) Các trung điểm của các cạnh của nó là các đỉnh của một khối tám mặt đều.
Giải
a)
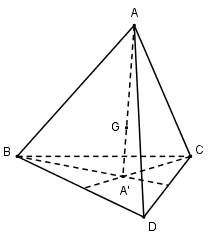
Gọi \(A’, B’, C’, D’\) lần lượt là trọng tâm của tam giác \(BCD, CDA, BDA, ABC\) của tứ diện đều \(ABCD\) có trọng tâm \(G\).
Ta có \(\overrightarrow {GA’} = – {1 \over 3}\overrightarrow {GA} \)
Gọi \({V_{\left( {G;{{ – 1} \over 3}} \right)}}\) là phép vị tự tâm \(G\) tỉ số \( – {1 \over 3}\) ta có \(A’, B’, C’, D’\) lần lượt là ảnh của \(A, B, C, D\) qua phép vị tự \(V\). Từ đó suy ra \({{A’B’} \over {AB}} = {{B’C’} \over {BC}} = {{C’D’} \over {CD}} = {{D’A’} \over {DA}} = {{A’C’} \over {AC}} = {{B’D’} \over {BD}} = {1 \over 3}\)
Do đó nếu \(ABCD\) là tứ diện đều thì \(A’B’C’D’\) cũng là tứ diện đều.
b)
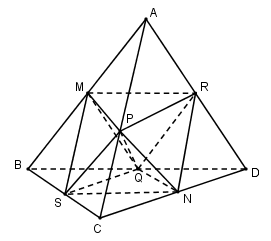
Gọi \(M, N, P, Q, R, S\) lần lượt là trung điểm của các cạnh \(AB, CD, AC, BD, AD, BC\) của khối tứ diện đều \(ABCD\). Khi đó, tám tam giác \(MPR, MRQ, MQS, MSP,\)\( NPR, NRQ, NQS, NSP\) là những tam giác đều, chúng làm thành khối đa diện với các đỉnh là \(M, N, P, Q, R, S\) mà mỗi đỉnh là đỉnh chung của bốn cạnh. Vậy đó là khối tám mặt đều.
Advertisements (Quảng cáo)
Bài 13: Hai đỉnh của một khối tám mặt đều được gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối tám mặt đều. Chứng minh rằng trong khối tám mặt đều :
a) Ba đường chéo cắt nhau tại trung điểm của mỗi đường ;
b) Ba đường chéo đôi một vuông góc với nhau ;
c) Ba đường chéo bằng nhau.
Giải
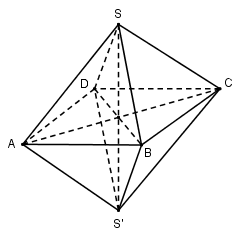
Giả sử \(SABCDS’\) là khối tám mặt đều. Ba đường chéo của nó là \(SS’, AC\) và \(BD\). Bốn điểm \(A, B, C, D\) cách đều hai điểm \(S\) và \(S’\) nên cùng nằm trên một mặt phẳng.
Advertisements (Quảng cáo)
Vậy \(ABCD\) là hình thoi, ngoài ra \(S\) cách đều \(A, B, C, D\) nên hình thoi đó là hình vuông. Suy ra hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm của mỗi đường, chúng vuông góc với nhau và có độ dài bằng nhau. Tương tự đối với các cặp đường chéo còn lại.
Bài 14: Chứng minh rằng :
a) Tâm các mặt của một khối lập phương là các đỉnh của một khối tám mặt đều ;
b) Tâm cảc mặt của một khối tám mặt đều là các đỉnh của một khối lập phương.
Giải
a) Gọi \(M, N, P, Q, R, S\) lần lượt là tâm của các mặt \(ABCD, A’B’C’D’, ABB’A’, \)\(CDD’C’, BCC’B’, ADD’A’\) của khối lập phương \(ABCD.A’B’C’D’\). Khi đó tám tam giác \(MPR, MRQ, MQS, MSP,\)\( NPR, NRQ, NQS, NSP\) là những tam giác đều, chúng làm thành khối đa diện với các đỉnh là \(M, N, P, Q, R, S\) mà mỗi đỉnh có \(4\) cạnh. Vậy đó là khối tám mặt đều.
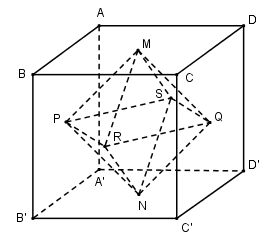
b) Cho khối tám mặt đều \(SABCDS’\). Gọi \(M, N, P, Q, M’, N’, P’, Q’\) lần lượt là trọng tâm của các mặt \(SAB, SBC, SCD, SAD, S’AB, S’BC, S’CD, S’DA\) thì các tứ giác \(MNPQ, M’N’P’Q’, MNN’M’\),\( PQQ’P’, NPP’N’, MQQ’M’\) đều là hình vuông và mỗi đỉnh \(M, N, P, Q, M’, N’, P’, Q’\) đều là đỉnh chung của 3 cạnh.
Vậy \(MNPQ.M’N’P’Q’\) là khối lập phương.
Chú ý: Giả sử cạnh của khối tám mặt đều là \(a\) thì khối lập phương \(MNPQ.M’N’P’Q’\) là \({2 \over 3}{{a\sqrt 2 } \over 2} = {{a\sqrt 2 } \over 3}\)

