Câu 1.1: Cho hình bs.4. Biết \(\overparen{DOA}\)= 1200, OA vuông góc với OC, OB vuông góc với OD.
a) Đọc tên các gốc ở tâm có số đo nhỏ hơn 1800.
b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 1800).
d) So sánh hai cung nhỏ AB và BC.
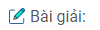
a) Các góc ở tâm có số đo nhỏ hơn 1800 là:
\(\widehat {AOB},\widehat {AOC},\widehat {AOD},\widehat {BOC},\widehat {BOD},\widehat {COD}\)
b) \(OA \bot OC \Rightarrow \widehat {AOC} = {90^0}\)
\(OB \bot OD \Rightarrow \widehat {BOD} = {90^0}\)
\(\widehat {AOB} + \widehat {BOD} = \widehat {AOD}\)
\( \Rightarrow \widehat {AOB} = \widehat {AOD} – \widehat {BOD} = {120^0} – {90^0} = {30^0}\)
\(\widehat {AOC} + \widehat {COD} = \widehat {AOD}\)
\( \Rightarrow \widehat {COD} = \widehat {AOD} – \widehat {AOC} = {120^0} – {90^0} = {30^0}\)
\(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\)
\( \Rightarrow \widehat {BOC} = \widehat {AOC} – \widehat {AOB} = {90^0} – {30^0} = {60^0}\)
c) Các cung có số đo bằng nhau nhỏ hơn 1800 là:
\(\overparen{AB}\) = \(\overparen{CD}\); \(\overparen{AC}\) = \(\overparen{BD}\)
d) sđ \(\overparen{AB}\)=\( = \widehat {AOB} = {30^0}\)
sđ \(\overparen{BC}\)\( = \widehat {BOC} = {60^0}\)
Advertisements (Quảng cáo)
Suy ra: sđ \(\overparen{BC}\) gấp đôi sđ \(\overparen{AB}\)
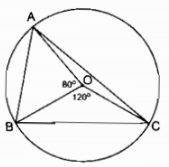
Câu 1.2: Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ \(\overparen{BC}\) = sđ \(\overparen{BA}\) ; sđ \(\overparen{BD}\) = \({1 \over 2}\) sđ \(\overparen{BA}\); sđ \(\overparen{BE}\) = \({2 \over 3}\) sđ \(\overparen{BA}\).
a) Đọc tên các góc ở tâm có số đo không lớn hơn 1800.
b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 1800).
d) So sánh hai cung nhỏ AE và BC.
a) Các góc ở tâm có số đo không quá 1800 là:
\(\widehat {AOB},\widehat {AOC},\widehat {AOD},\widehat {AOE},\widehat {BOC},\widehat {BOD},\)
\(\widehat {BOE},\widehat {COD},\widehat {COE},\widehat {DOE}\)
b) \(\widehat {AOB} = {180^0}\)
sđ \(\overparen{AB}\) = 1800
Advertisements (Quảng cáo)
Ta có: sđ \(\overparen{BC}\) = \( = {1 \over 6}\) sđ \(\overparen{AB}\)
= \({1 \over 6}{.180^0}\) = 300
\( \Rightarrow \widehat {BOC} = \) sđ \(\overparen{BC}\) = 300
Ta có: sđ \(\overparen{BD}\) \( = {1 \over 2}\)sđ \(\overparen{AB}\)
= \({1 \over 2}{.180^0} = {90^0}\)
\( \Rightarrow \widehat {BOD} = \)sđ \(\overparen{BD}\) = \({90^0}\)
Ta có: sđ \(\overparen{BE}\) \( = {2 \over 3}\) sđ \(\overparen{BA}\)
\( = {2 \over 3}{.180^0} = {120^0}\)
\( \Rightarrow \widehat {BOE} = \) sđ \(\overparen{BE}\) = 1200
\(\widehat {BOC} + \widehat {COE} = \widehat {BOE}\)
\( \Rightarrow \widehat {COE} = \widehat {BOE} – \widehat {BOC}\)
\( = {120^0} – {30^0} = {90^0}\)
\(\widehat {AOE} + \widehat {BOE} = \widehat {AOB}\)
\( \Rightarrow \widehat {AOE} = \widehat {AOB} – \widehat {BOE}\)
\( = {180^0} – {120^0} = {60^0}\)
\(\widehat {AOD} = \widehat {BOD} = {1 \over 2}\widehat {AOB} = {90^0}\)
\(\widehat {BOC} + \widehat {COD} = \widehat {BOD}\)
\( \Rightarrow \widehat {COD} = \widehat {BOD} – \widehat {BOC}\)
= \({90^0} – {30^0} = {60^0}\)
\(\widehat {COD} + \widehat {DOE} = \widehat {COE}\)
\( \Rightarrow \widehat {DOE} = \widehat {COE} – \widehat {COD}\)
\( = {90^0} – {60^0} = {30^0}\)
c) Các cung có số đo nhỏ hơn 1800 bằng nhau.
\(\overparen{BC}\)= \(\overparen{DE}\); \(\overparen{AE}\) = \(\overparen{CD}\); \(\overparen{AD}\) = \(\overparen{BD}\).
\(\overparen{AC}\) = \(\overparen{BE}\); \(\overparen{AD}\) = \(\overparen{CE}\); \(\overparen{CE}\) = \(\overparen{BD}\).
d) sđ \(\overparen{AE}\) \( = \widehat {AOE} = {60^0}\)
sđ \(\overparen{BC}\)\( = \widehat {BOC} = {30^0}\)
Ta có số đo của cung \(\overparen{AE}\) gấp đôi số đo của cung \(\overparen{BC}\).

