Câu 6.1: Dựng một cung chứa góc 600 trên đoạn thẳng AB cho trước.
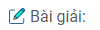
Cách dựng: − Dựng đoạn thẳng AB.
− Dựng tia Ax sao cho \(\widehat {BAx} = 60^\circ \).
− Dựng đường thẳng d là trung trực của AB.
− Dựng tia Ay ⊥ Ax tại A.
− Tia Ay cắt đường thẳng d tại O.
− Dựng cung tròn tâm O bán kính OA.
− Dựng O’ đối xứng với O qua AB.
− Dựng cung tròn tâm O’ bán kính O’A.
Ta có cung chứa góc 60º vẽ trên đoạn AB cho trước.
Câu 6.2: Cho đường tròn tâm O bán kính R và điểm A (khác O) ở trong đường tròn đó. Một đường thẳng d thay đổi, luôn đi qua A, cắt đường tròn đã cho tại hai điểm là B và C. Tìm quỹ tích trung điểm I của đoạn thẳng BC.
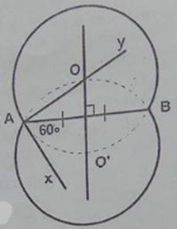
Chứng minh thuận:
Đường tròn (O) cho trước, điểm A cố định nên OA có độ dài không đổi.
Advertisements (Quảng cáo)
∆OBC cân tại O (vì OB = OC bán kính)
IB = IC (gt) nên OI là đường trung tuyến vừa là đường cao
\( \Rightarrow \) OI ⊥ BC
\( \Rightarrow \widehat {OIA} = 90^\circ \)
Đường thẳng d thay đổi nên B, C thay đổi thì I thay đổi tạo với 2 đầu đoạn OA cố định góc \(\widehat {OIA} = 90^\circ \). Vậy I chuyển động trên đường tròn đường kính OA.
Chứng minh đảo: Lấy điểm I’ bất kỳ trên đường tròn đường kính AO. Đường thẳng AI’ cắt đường tròn (O) tại 2 điểm B’ và C’.
Ta chứng minh: I’B = I’C’.
Trong đường tròn đường kính AO ta có \(\widehat {OI’A} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \) OI’⊥ B’C’
\( \Rightarrow \) I’B’ = I’C’ (đường kính vuông góc với dây cung)
Vậy quỹ tích các điểm I là trung điểm của dây BC của đường tròn tâm O khi BC quay xung quanh điểm A cố định là đường tròn đường kính AO.
Advertisements (Quảng cáo)
Câu 6.3: Cho tam giác ABC có ba góc nhọn. Xác định vị trí của điểm M trong tam giác sao cho \(MA + MB + MC\) nhỏ nhất.
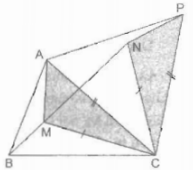
Trong ∆ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC.
Xét ∆AMC và ∆PNC:
CM = CN (vì ∆MCN đều)
CA = CP (vì ∆APC đều)
\(\widehat {MCA} + \widehat {ACN} = 60^\circ \)
\(\widehat {ACN} + \widehat {NCP} = 60^\circ \)
\( \Rightarrow \widehat {MCA} = \widehat {NCP}\)
Suy ra: ∆AMC = ∆PNC (c.g.c)
\( \Rightarrow \) PN = AM
MA + MB + MC = MB + MN + NP
Ta có ∆ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.
Vì \(\widehat {CMN} = 60^\circ \) nên 3 điểm B, M, N thẳng hàng khi và chỉ khi \(\widehat {BMC} = 120^\circ \)
Vì \(\widehat {CNM} = 60^\circ \) nên 3 điểm M, N, P thẳng hàng khi và chỉ khi \(\widehat {CNP} = 120^\circ \)
Mà ∆AMC = ∆PNC (chứng minh trên) \( \Rightarrow \widehat {AMC} = \widehat {PNC} = 120^\circ \)
Vậy MA + MB + MC bé nhất khi và chỉ khi \(\widehat {BMC} = 120^\circ \) và \(\widehat {AMC} = 120^\circ \)
Vậy M là giao điểm của 2 cung chứa góc 120º dựng trên BC và AC.

