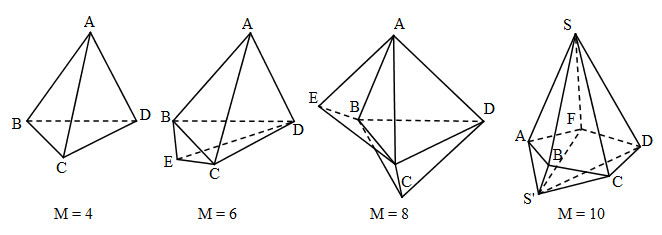
Bài 1: Chứng minh rằng nếu khối đa diện có các mặt là tam giác thì số mặt phải là số chẵn. Hãy chỉ ra những khối đa diện như thế với số mặt bằng \(4, 6, 8, 10\).
Giải
Gọi số cạnh của khối đa diện là \(C\), số mặt là \(M\). Vì mỗi mặt có ba cạnh và mỗi cạnh lại chung cho hai mặt bên nên \(3M = 2C\). Suy ra \(M\) là số chẵn.
Sau đây là một số khối đa diện có các mặt là tam giác.
Bài 2: Chứng minh rằng nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn.
Giải
Advertisements (Quảng cáo)
Gọi số cạnh của khối đa diện là \(C\), số đỉnh là \(Đ\). Vì mỗi đỉnh là đỉnh chung của ba cạnh và mỗi cạnh có \(2\) đỉnh nên \(3Đ = 2C\) do đó \(Đ\) là sỗ chẵn.
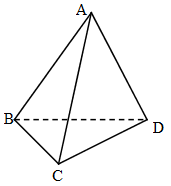
Bài 3: Chứng minh rằng nếu khối đa diện có các mặt là tam giác và mỗi đỉnh là đỉnh chung của ba cạnh thì đó là khối tứ diện.
Giải
Advertisements (Quảng cáo)
Gọi \(A\) là một đỉnh của khối tứ diện. Theo giả thiết đỉnh \(A\) là đỉnh chung của \(3\) cạnh, ta gọi \(3\) cạnh đó là \(AB, AC, AD\). Cạnh \(AB\) phải là cạnh chung của hai mặt tam giác, đó là hai mặt \(ABC\) và \(ABD\) (Vì qua đỉnh \(A\) chỉ có \(3\) cạnh). Tương tự, ta có các mặt tam giác \(ACD\) và \(BCD\). Vậy khối đa diện đó chính là khối tứ diện \(ABCD\).
Bài 4: Hãy phân chia một khối hộp thành năm khối tứ diện.
Giải
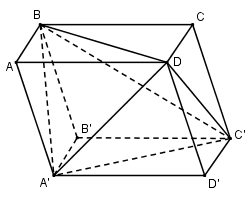
Có thể phân chia khối hộp \(ABCD.A’B’C’D’\) thành năm khối tứ diện \(ABDA’ ; CBDC’ ; B’A’C’B ; D’A’C’D ; BDA’C’.\)
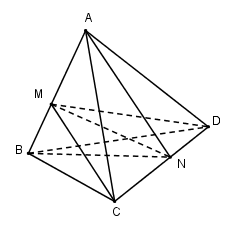
Bài 5: Hãy phân chia một khối tứ diện thành bốn khối tứ diện bởi hai mặt phẳng.
Giải
Cho khối tứ diện \(ABCD\). Lấy điểm \(M\) nằm giữa \(A\) và \(B\), điểm \(N\) nằm giữa \(C\) và \(D\). Bằng hai mặt phẳng \((MCD)\) và \((NAB)\) ta chia khối tứ diện đã cho thành \(4\) khối tứ diện: \(AMCN ; AMND ; BMCN ; BMND\).