Câu 68: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD.
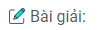
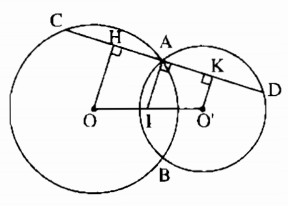
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra: OH // IA // O’K
Theo giả thiết: IO = IO’
Suy ra: AH = AK ((tính chất đường thẳn
g song song cách đều) (1)
Ta có: OH ⊥ AC
Suy ra: \(HA = HC = {1 \over 2}AC\) (đường kính dây cung) ⇒AC = 2AH (2)
Lại có: O’K ⊥ AD.
Suy ra: \(KA = KD = {1 \over 2}AD\) ( đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD.
Câu 69: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O).
a) Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (O’)
b) Đường vuông góc với AO’ tại O’ cắt AB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng.
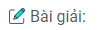
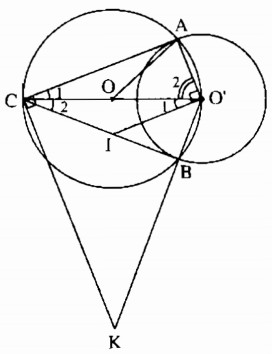
a) Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên \(\widehat {O’AC} = 90^\circ \)
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên \(\widehat {O’BC} = 90^\circ \)
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến đường tròn (O’)
b) Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C.
Advertisements (Quảng cáo)
Suy ra: \(\widehat {ACO’} = \widehat {BCO’}\) (tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA \( \Rightarrow \widehat {ACO’} = \widehat {CO’I}\) (hai góc so le trong)
Suy ra: \(\widehat {BCO’} = \widehat {CO’I}\)
Hay tam giác CIO’ cân tại I ⇒ IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: \(\widehat {AO’C} = \widehat {BO’C}\) (tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A \(\Rightarrow \widehat {AO’C} = \widehat {O’CK}\) (hai góc so le trong)
Suy ra: \(\widehat {O’CK} = \widehat {KO’C}\)
Hay tam giác CKO’ cân tại K ⇒ KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C.
Advertisements (Quảng cáo)
Vậy O, I, K thẳng hàng.
Câu 70: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường tròn (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng:
a) AB ⊥ KB;
b) Bốn điểm A, C, E, D nằm trên cùng một đường tròn.
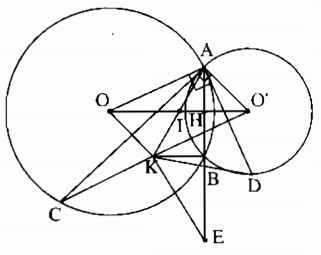
a) Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H
Ta có: HA = HB
I là trung điểm của OO’ nên IH ⊥ AB (1)
Trong tam giác ABK, ta có:
HA = HB (chứng minh trên)
IA = IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH // BK (2)
Từ (1) và (2) suy ra: AB ⊥KB
b) Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE ( tính chất đối xứng tâm)
Suy ra: KA = KE ( tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK ( chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đườngg tròn (O’))
OK // O’A ( chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC ( tính chất đường trung trực) (4)
DA ⊥ OA ( vì DA là tiếp tuyến của đường tròn (O))
O’K // OA ( chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD ( tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.

