Câu 56: Từ đỉnh một ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới gốc 30° so với đường nằm ngang chân đèn. Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu?
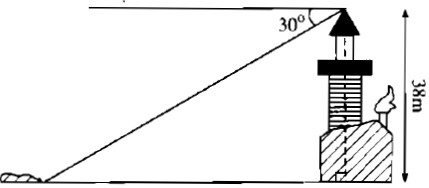

Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30° , chiều cao của cột đèn biển là cạnh đối diện với góc 30° .
Vậy khoảng cách từ đảo đến chân đèn là:
\(38.\cot g30^\circ \approx 65,818\left( {cm} \right)\)
Câu 57: Trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1
Trong tam giác ABC có \(AB = 11cm,\widehat {ABC} = 38^\circ ,\widehat {ACB} = 30^\circ \). N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC.


Trong tam giác vuông ABN, ta có:
\(AN = AB.\sin \widehat B = 11.\sin 38^\circ \approx 6,772\left( {cm} \right)\)
Trong tam giác vuông ACN, ta có:
\(AC = {{AN} \over {\sin \widehat C}} \approx {{6,772} \over {\sin 30^\circ }} = 13,544\left( {cm} \right)\)
Câu 58:Trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1
Để nhìn thấy đỉnh A của một vách đá dựng đứng, người ta đã đứng tại điểm P cách chân vách đá một khoảng 45m và nhìn lên một góc 25° so với đường nằm ngang (góc nhìn lên này được gọi là góc “nâng”). Hãy tính độ cao của vách đá.
Advertisements (Quảng cáo)


Chiều cao vách đá là cạnh góc vuông đối diện với góc 25° . Khi đó chiều cao của vách đá là:
\(45.tg25^\circ \approx 20,984\left( m \right)\)
Câu 59: Tìm x và y trong các hình sau

a) Hình a

Trong tam giác vuông ACP,ta có:
\(x = CP = AC.\sin \widehat A\)
Advertisements (Quảng cáo)
\( = 8.\sin 30^\circ = 8.{1 \over 2} = 4\)
Trong tam giác vuông BCP, ta có:
\(y = BC = {x \over {\cos \widehat {BCP}}} = {4 \over {{\rm{cos50}}^\circ }} \approx 6,223\)
b) Hình b
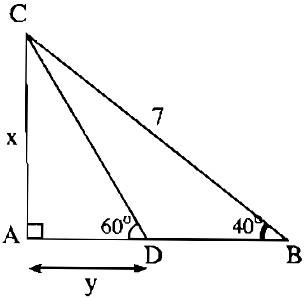
Trong tam giác vuông ABC, ta có:
\(x = AC = BC.\sin \widehat B\)
\( = 7.\sin 40^\circ \approx 4,5\)
Trong tam giác vuông ACD, ta có:
\(y = AD = AC.\cot g\widehat D\)
\( \approx 4,5\cot g60^\circ = 2,598\)
c) Hình c

Vì tứ giác CDPQ có hai góc vuông và hai cạnh CD = DP = 4 nên nó là hình vuông. Suy ra: CD = DP = PQ = QC = 4
Trong tam giác vuông BCQ, ta có:
\(x = BC = {{CQ} \over {{\rm{cos}}\widehat {BCQ}}} = {4 \over {{\rm{cos50}}^\circ }} \approx 6,223\)
\(BQ = BC.\sin \widehat {BCQ} \approx 6,223.\sin 50^\circ = 4,767\)
Trong tam giác vuông ADP, ta có:
\(AP = DP.\cot gA = 4.\cot g70^\circ \approx 1,456\)
Ta có:
\(y = AB = AP + PQ + QB\)
\(= 1,456 + 4 + 4,767 = 10,223\).

