Câu 6.1: Độ dài mỗi cạnh của tam giác đều ngoại tiếp đường tròn (O ; r) bằng
(A) \(r\sqrt 3 \) ; (B) \(2r\sqrt 3 \) ;
(B) (C) 4r ; (D) 2r.
Hãy chọn phương án đúng.

Chọn (B).
Advertisements (Quảng cáo)
Câu 6.2: Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Đường thẳng đi qua O và song song với AB cắt AC tại D. Đường tròn đi qua O và song song với AC cắt AB ở E. Tứ giác ADOE là hình gì ?


ADOE là hình bình hành, lại có AO là đường phân giác của góc A nên là hình thoi.
Advertisements (Quảng cáo)
Câu 6.3: Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD.

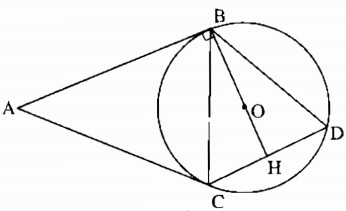
Ta có OB ⊥ AB và AB // CD nên OB ⊥ CD. Gọi H là giao điểm của BO và CD thì BH ⊥ CD, suy ra HC = HD. Do đó BC = BD.

