Câu 23: Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. hãy cho biết ACBD là hình gì? Vì sao?
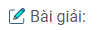
Ta có: OI ⊥ CD (gt)
Suy ra: IC = ID (đường kính dây cung)
Mà: IA = IB (gt)
Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Câu 2.1: Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng
(A) \({R \over 2}\) ; (B) \({{R\sqrt 3 } \over 2}\) ;
(B) (C) \(R\sqrt 3 \) ; (D) Một đáp số khác.
Advertisements (Quảng cáo)
Hãy chọn phương án đúng.
Chọn (C).
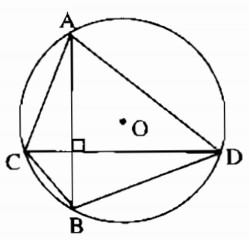
Câu 2.2: Cho đường tròn (O; 2cm). Vẽ hai dây AB và CD vuông góc với nhau. Tính diện tích lớn nhất của tứ giác ABCD
Advertisements (Quảng cáo)
Ta có \(AB \le 4cm\),
\(CD \le 4cm.\) Do AB ^ CD nên
\({S_{ABCD}} = {1 \over 2}AB.CD \le {1 \over 2}.4.4 = 8\) (cm2).
Giá trị lớn nhất của \({S_{ABC{\rm{D}}}}\) bằng 8 cm2 khi AB và CD đều là đường kính của đường tròn.
Câu 2.3: Cho đường tròn (O; R), dây AB khác đường kính. Vẽ về hai phía của AB các dây AC, AD. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ B và AC và AD. Chứng minh rằng:
a) Bốn điểm A, H, B, K thuộc cùng một đường tròn;
b) HK < 2R.
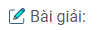
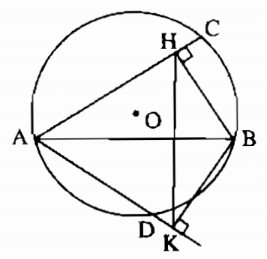
a) Bốn điểm A, H, B, K cùng thuộc đường tròn đường kính AB.
b) Ta có \(HK \le AB \le 2R\).

