Câu 11: Cho hàm số \(y = a{x^2}\)
a) Xác định hệ số a biết rằng đồ thị của nó cắt đường thẳng \(y = – 2x + 3\) tại điểm A có hoành độ bằng 1.
b) Vẽ đồ thị của hàm số \(y = – 2x + 3\) và của hàm số \(y = a{x^2}\) với giá trị của a vừa tìm được trong câu a trên cùng một mặt phẳng tọa độ.
c) Nhờ đồ thị xác định tọa độ của giao điểm thứ hai của hai đồ thị vừa vẽ trong câu b.
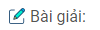
a) Điểm A thuộc đồ thị hàm số \(y = – 2x + 3\) nên tọa độ của A nghiệm đúng phương trình đường thẳng: \(y = – 2.1 + 3 = 1\) điểm A (1; 1)
Điểm A (1; 1) thuộc đồ thị hàm số \(y = a{x^2}\) nên tọa độ của điểm A nghiệm đúng phương trình hàm số: \(1 = a{.1^2} \Leftrightarrow a = 1\)
Hàm số đã cho: \(y = {x^2}\)
b) Vẽ đồ thị hàm số: \(y = {x^2}\)
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| \(y = {x^2}\) |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
Vẽ đồ thị \(y = – 2x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) B (0; 3)
A (1; 1)
c) Giao điểm thứ hai A’ của đường thẳng và parabol có hoành độ x = -3; tung độ y = 9 A’ (-3; 9)
Câu 12: Cho hàm số \(y = {3 \over 4}{x^2}\)
a) Vẽ đồ thị của hàm số.
Advertisements (Quảng cáo)
b) Tìm trên đồ thị điểm A có hoành độ bằng -2. Bằng đồ thị, tìm tung độ của A.
c) Tìm trên đồ thị các điểm có tung độ bằng 4. Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách:
– Ước lượng trên đồ thị;
– Tính theo công thức \(y = {3 \over 4}{x^2}\)
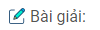
a) Vẽ đồ thị hàm số \(y = {3 \over 4}{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
3 |
| \(y = {3 \over 4}{x^2}\) |
3 |
\({3 \over 4}\) |
0 |
\({3 \over 4}\) |
2 |
b) Từ điểm x = -2 kẻ đường thẳng song song với trục tung cắt đồ thị tại A.
Từ A kẻ đường thẳng song song với trục hoành cắt trục tung tại điểm có tung độ y = 3; A (-2; 3)
Advertisements (Quảng cáo)
c) Từ điểm có tung độ y = 4 kẻ đường thẳng song song với trục hoành cắt đồ thị tại B và B’ là điểm có tung độ y = 4.
Từ B và B’ kẻ đường thẳng song song với trục tung cắt trục hoành tại điểm có hoành độ \(x \approx – 2;x \approx 2\)
Thay y = 4 ta có: \(4 = {3 \over 4}{x^2} \Leftrightarrow {x^2} = {{16} \over 3} \Leftrightarrow x = \pm {{4\sqrt 3 } \over 3} \approx \pm 2,3\)
Câu 13: Cho hàm số \(y = f\left( x \right) = – 1,5{x^2}\)
a) Vẽ đồ thị của hàm số.
b) Không làm tính, dùng đồ thị để so sánh f(-1,5) và f(-0,5), f(0,75) và f(1,5).
c) Dùng đồ thị, tìm những giá trị thích hợp điền vào các chỗ (…):
Khi thì… ≤ y ≤ …
Khi -2 ≤ x ≤ 0 thì …≤ y ≤ …
Khi -2 ≤ x ≤ 1 thì … ≤ y ≤ …
a) Vẽ đồ thị hàm số \(y = f\left( x \right) = – 1,5{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
2 |
| \(y = f\left( x \right) = – 1,5{x^2}\) |
-6 |
-1,5 |
0 |
-1,5 |
-6 |
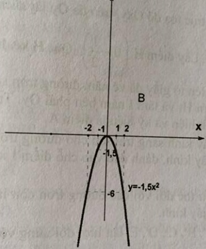
b) Hàm số \(y = – 1,5{x^2}\)
\(a = – 1,5 < 0\)
Hàm số đồng biến trong x < 0, nghịch biến trong \(x > 0 \Rightarrow f\left( { – 1,5} \right) < f\left( { – 0,5} \right)\)
\(f\left( {0,75} \right) > f\left( {1,5} \right)\)
c) Khi \(1 \le x \le 2\) thì -6 ≤ y ≤ -1,5
Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0
Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0

