Câu 2.1: Parabol \(y = a{x^2}\) trong hình vẽ có hệ số a là bao nhiêu?
A) 1
B) -1
C) 2
D) \({1 \over 2}\)
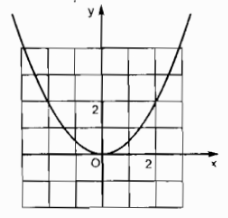
Parabol \(y = {x^2}\) trong hình vẽ có hệ số a bằng
Chọn D) \({1 \over 2}\)
Vì điểm có hoành độ x = 2 thì tung độ y = 2 nên \(a = {y \over {{x^2}}} = {2 \over {{2^2}}} = {1 \over 2}\)
Câu 2.2: Cho hàm số \(y = 0,5{x^2}\)
a) Tìm các giá trị của x để y < 2.
b) Tìm các giá trị của x để y > 2.
c) Tìm các giá trị của y khi -2 < x < 2
d) Tìm các giá trị của y khi x ≤ 0.
Advertisements (Quảng cáo)
e) Tìm các giá trị của y khi x ≤ 2.
a) Để giá trị y < 2 thì -2 < x < 2
b) Để giá trị y > 2 thì x > 2 hoặc x < -2
c) Khi -2 < x < 2 thì 0 ≤ y ≤ 2
d) Khi x ≤ 0 thì y ≥ 0
e) Khi x ≤ 2 thì y ≥ 0
Câu 2.3:
a) Xác định hàm số \(y = a{x^2}\) và vẽ đồ thị của nó, biết rằng đồ thị của nó đi qua điểm A (-1; 2).
b) Xác định đường thẳng \(y = a’x + b’\) biết rằng đường thẳng này cắt đồ thị của hàm số vừa tìm được trong câu a tại điểm A và điểm B có tung độ là 8.
Advertisements (Quảng cáo)
a) Đồ thị hàm số đi qua A (-1; 2) nên tọa độ của A nghiệm đúng phương trình hàm số: \(2 = a{\left( { – 1} \right)^2} \Leftrightarrow a = 2\)
Hàm số đã cho: \(y = 2{x^2}\)
Vẽ đồ thị hàm số: \(y = 2{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
2 |
| \(y = 2{x^2}\) |
8 |
2 |
0 |
2 |
8 |
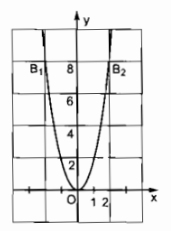
b) Khi y = 8 suy ra: \(2{x^2} = 8 \Rightarrow x = \pm 2\)
Do đó ta có: \({B_1}\left( { – 2;8} \right)\) và \({B_2}\left( {2;8} \right)\)
Đường thẳng \(y = a’x + b\) đi qua A và B1 nên tọa độ của A và B1 nghiệm đúng phương trình.
Điểm A: \( – 2 = – a’ + b’\)
Điểm B: \(8 = – 2a’ + b’\)
Hai số a’ và b’ là nghiệm của hệ phương trình:
\(\eqalign{
& \left\{ {\matrix{
{ – a’ + b’ = 2} \cr
{ – 2a’ + b’ = 8} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{ – a’ = 6} \cr
{ – a’ + b’ = 2} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{a’ = – 6} \cr
{6 + b’ = 2} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{a’ = – 6} \cr
{b’ = – 4} \cr} } \right. \cr} \)
Phương trình đường thẳng AB1 là \(y = – 6x – 4\)
Đường thẳng \(y = a’x + b’\) đi qua A và B2 nên tọa độ của A và B2 nghiệm đúng phương trình đường thẳng.
Điểm A: 2 = -a’ + b’
Điểm B2: 8 = 2a’ + b’
Hai số a’ và b’ là nghiệm của hệ phương trình
\(\eqalign{
& \left\{ {\matrix{
{ – a’ + b’ = 2} \cr
{2a’ + b’ = 8} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{3a’ = 6} \cr
{ – a’ + b’ = 2} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{a’ = 2} \cr
{ – 2 + b’ = 2} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{a’ = 2} \cr
{b’ = 4} \cr} } \right. \cr} \)
Phương trình đường thẳng AB2 là \(y = 2x + 4.\)

