Câu 63: Cho tam giác ABC vuông cân có AB = AC = 12cm. Điểm M chạy trên AB) Tứ giác MNCP là một hình bình hành có đỉnh N thuộc cạnh AC (h.6). Hỏi khi M cách A bao nhiêu thì diện tích của hình bình hành bằng 32cm2?
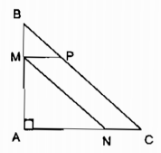
Gọi độ dài đoạn MA = x cm; điều kiện 0 < x < 12
Vì ∆ ABC vuông cân tại A nên tam giác BMP vuông cân tại M
⇒ MP = MB = AB – AM = 12 – x (cm)
Diện tích hình bình hành MNCP bằng MP.MA
Suy ra: MP.MA = (12 – x)x
Ta có phương trình:
\(\eqalign{
& \left( {12 – x} \right)x = 32 \cr
& \Rightarrow {x^2} – 12x + 32 = 0 \cr
& \Delta ‘ = {\left( { – 6} \right)^2} – 1.32 = 36 – 32 = 4 > 0 \cr
& \sqrt {\Delta ‘} = \sqrt 4 = 2 \cr
& {x_1} = {{6 + 2} \over 1} = 8 \cr
& {x_2} = {{6 – 2} \over 1} = 4 \cr} \)
Cả hai giá trị x1 = 8 và x2 = 4 thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A là 8cm hoặc 4cm
Câu 64: Chu vi bánh sau của một máy cày lớn hơn chu vi bánh trước là 1,5m. Khi đi trên đoạn đường dài 100m thì bánh trước quay nhiều hơn bánh sau 15 vòng. Tính chu vi của mỗi bánh xe.
Gọi chu vi của bánh trước là x (m), điều kiện: x > 0
Chu vi của bánh sau là x + 1,5 (m)
Số vòng quay của bánh trước là \({{100} \over x}\) vòng
Số vòng quay của bánh sau là \({{100} \over {x + 1,5}}\) vòng
Advertisements (Quảng cáo)
Ta có phương trình:
\(\eqalign{
& {{100} \over x} – {{100} \over {x + 1,5}} = 15 \cr
& \Rightarrow 100\left( {x + 1,5} \right) – 100x = 15x\left( {x + 1,5} \right) \cr
& \Leftrightarrow 100x + 150 – 100x = 15{x^2} + 22,5x \cr
& \Leftrightarrow 15{x^2} + 22,5x – 150 = 0 \cr
& \Leftrightarrow 2{x^2} + 3x – 20 = 0 \cr
& \Delta = {3^2} – 4.2.\left( { – 20} \right) = 9 + 160 = 169 > 0 \cr
& \sqrt \Delta = \sqrt {169} = 13 \cr
& {x_1} = {{ – 3 + 13} \over {2.2}} = 2,5 \cr
& {x_2} = {{ – 3 – 13} \over {2.2}} = – 4 \cr} \)
x2 = -4 < 0 không thỏa mãn điều kiện: loại.
Vậy chu vi bánh xe trước bằng 2,5m
Chu vi bánh xe sau bằng 2,5 + 1,5 = 4m
Câu 65: Bài toán cổ Ấn Độ
Một đàn khỉ chia thành hai nhóm.
Nhóm chơi đùa vui vẻ ngoài trời
Bằng bình phương một phần tám của đàn.
Mười hai con nhảy nhót trên cây.
Không khí tươi vui sưởi ấm nơi này.
Advertisements (Quảng cáo)
Hỏi có tất cả bao nhiêu con khỉ?
Gọi số khỉ của đàn là x (con)
Điều kiện: x ∈ N* và x ⋮ 8
Nhóm chơi đùa ngoài trời có \({\left( {{x \over 8}} \right)^2}\) con
Nhóm nhảy nhót trên cây là 12 con
Ta có phương trình:
\(\eqalign{
& x = {\left( {{x \over 8}} \right)^2} + 12 \cr
& \Leftrightarrow x = {{{x^2}} \over {64}} + 12 \cr
& \Leftrightarrow {x^2} – 64x + 768 = 0 \cr
& \Delta ‘ = {\left( { – 32} \right)^2} – 1.768 = 1024 – 768 = 256 > 0 \cr
& \sqrt {\Delta ‘} = \sqrt {256} = 16 \cr
& {x_1} = {{32 + 16} \over 1} = 48 \cr
& {x_2} = {{32 – 16} \over 1} = 16 \cr} \)
Cả hai giá trị x1 = 48 và x2 = 16 thỏa mãn điều kiện bài toán
Vậy đàn khỉ có 48 con hoặc 16 con
Câu 66: Bài toán của Ơ-le
Hai nông dân đem 100 quả trứng ra chợ bán. Số trứng của hai người không bằng nhau, nhưng hai người bán được số tiền bằng nhau. Một người nói với người kia: “Nếu số trứng của tôi bằng số trứng của anh thì tôi bán được 15 đồng”. Người kia nói: “Nếu số trứng của tôi bằng số trứng của anh thì tôi chỉ bán được \(6{2 \over 3}\) đồng thôi”. Hỏi mỗi người có bao nhiêu trứng?
Gọi số trứng của người thứ nhất là x (quả)
Điều kiện: x ∈ N* và x < 100
Thì số trứng của người thứ hai là 100 – x (quả)
Giá tiền một quả trứng của người thứ nhất: \({{15} \over {100 – x}}\) đồng
Giá tiền một quả trứng của người thứ hai \({{20} \over {3x}}\) đồng
Số tiền người thứ nhất thu được là \({{15} \over {100 – x}}.x = {{15x} \over {100 – x}}\) đồng
Số tiền người thứ hai thu được là: \({{20} \over {3x}}.\left( {100 – x} \right) = {{20\left( {100 – x} \right)} \over {3x}}\) đồng
Ta có phương trình:
\(\eqalign{
& {{15x} \over {100 – x}} = {{20\left( {100 – x} \right)} \over {3x}} \cr
& \Leftrightarrow 45{x^2} = 20{\left( {100 – x} \right)^2} \cr
& \Leftrightarrow 45{x^2} = 20\left( {10000 – 200x + {x^2}} \right) \cr
& \Leftrightarrow 45{x^2} = 200000 – 4000x + 20{x^2} \cr
& \Leftrightarrow 25{x^2} + 4000x – 200000 = 0 \cr
& \Leftrightarrow {x^2} + 160x – 8000 = 0 \cr
& \Delta ‘ = {80^2} – 1.\left( { – 8000} \right) = 6400 + 8000 = 14400 > 0 \cr
& \sqrt {\Delta ‘} = \sqrt {14400} = 120 \cr
& {x_1} = {{ – 80 + 120} \over 1} = 40 \cr
& {x_2} = {{ – 80 – 120} \over 1} = – 200 \cr} \)
Giá trị x2 = -200 ∉ N* không thỏa mãn điều kiện: loại.
Vậy: số trứng người thứ nhất là 40 quả
Số trứng người thứ hai là 60 quả.

