Câu 36: Hãy làm các phép chia sau :
a. \({{7x + 2} \over {3x{y^3}}}:{{14x + 4} \over {{x^2}y}}\)
b. \({{8xy} \over {3x – 1}}:{{12x{y^3}} \over {5 – 15x}}\)
c. \({{27 – {x^3}} \over {5x + 5}}:{{2x – 6} \over {3x + 3}}\)
d. \(\left( {4{x^2} – 16} \right):{{3x + 6} \over {7x – 2}}\)
e. \({{3{x^3} + 3} \over {x – 1}}:\left( {{x^2} – x + 1} \right)\)
a. \({{7x + 2} \over {3x{y^3}}}:{{14x + 4} \over {{x^2}y}}\)\( = {{7x + 2} \over {3x{y^3}}}.{{{x^2}y} \over {14x + 4}} = {{\left( {7x + 2} \right){x^2}y} \over {3x{y^3}.2\left( {7x + 2} \right)}} = {x \over {6{y^2}}}\)
b. \({{8xy} \over {3x – 1}}:{{12x{y^3}} \over {5 – 15x}}\)\( = {{8xy} \over {3x – 1}}.{{5 – 15x} \over {12x{y^3}}} = {{8xy\left( {5 – 15x} \right)} \over {\left( {3x – 1} \right).12x{y^3}}} \)
\(
= {{ – 10\left( {3x – 1} \right)} \over {3\left( {3x – 1} \right){y^2}}} = {{10} \over {3{y^2}}}\)
c. \({{27 – {x^3}} \over {5x + 5}}:{{2x – 6} \over {3x + 3}}\)\( = {{27 – {x^3}} \over {5x + 5}}:{{3x + 3} \over {2x – 6}} = {{\left( {{3^3} – {x^3}} \right).3\left( {x + 1} \right)} \over {5\left( {x + 1} \right).2\left( {x – 3} \right)}}\)
\( = {{ – 3\left( {x – 3} \right)\left( {{x^2} + 3x + 9} \right)} \over {10\left( {x – 3} \right)}} = – {{3\left( {{x^2} + 3x + 9} \right)} \over {10}}\)
d. \(\left( {4{x^2} – 16} \right):{{3x + 6} \over {7x – 2}}\)
\( = \left( {4{x^2} – 16} \right).{{7x – 2} \over {3x + 6}} = {{4\left( {x + 2} \right)\left( {x – 2} \right)\left( {7x – 2} \right)} \over {3\left( {x + 2} \right)}}\)
\( = {{4\left( {x – 2} \right)\left( {7x – 2} \right)} \over 3}\)
Advertisements (Quảng cáo)
e. \({{3{x^3} + 3} \over {x – 1}}:\left( {{x^2} – x + 1} \right)\)\( = {{3{x^3} + 3} \over {x – 1}}.{1 \over {{x^2} – x + 1}} \)
\(
= {{3\left( {{x^3} + 1} \right)} \over {\left( {x – 1} \right)\left( {{x^2} – x + 1} \right)}} = {{3\left( {x + 1} \right)\left( {{x^2} – x + 1} \right)} \over {\left( {x – 1} \right)\left( {{x^2} – x + 1} \right)}}\)
\( = {{3\left( {x + 1} \right)} \over {x – 1}}\)
Câu 37: Thực hiện phép tính ( chú ý đến quy tắc đổi dấu)
a. \({{4\left( {x + 3} \right)} \over {3{x^2} – x}}:{{{x^2} + 3x} \over {1 – 3x}}\)
b. \({{4x + 6y} \over {x – 1}}:{{4{x^2} + 12xy + 9{y^2}} \over {1 – {x^3}}}\)
a. \({{4\left( {x + 3} \right)} \over {3{x^2} – x}}:{{{x^2} + 3x} \over {1 – 3x}}\)\( = {{4\left( {x + 3} \right)} \over {3{x^2} – x}}.{{1 – 3x} \over {{x^2} + 3x}} \)
\(
= {{4\left( {x + 3} \right)\left( {1 – 3x} \right)} \over {x\left( {3x – 1} \right).x\left( {x + 3} \right)}} = {{ – 4\left( {3x – 1} \right)} \over {{x^2}\left( {3x – 1} \right)}} = – {4 \over {{x^2}}}\)
Advertisements (Quảng cáo)
b. \({{4x + 6y} \over {x – 1}}:{{4{x^2} + 12xy + 9{y^2}} \over {1 – {x^3}}} = \)\({{4x + 6y} \over {x – 1}}.{{1 – {x^3}} \over {4{x^2} + 12xy + 9{y^2}}} \)
\(
= {{2\left( {2x + 3y} \right)\left( {1 – x} \right)\left( {1 + x + {x^2}} \right)} \over {\left( {x – 1} \right){{\left( {2x + 3y} \right)}^2}}}\)
\( = – {{2\left( {x – 1} \right)\left( {1 + x + {x^2}} \right)} \over {\left( {x – 1} \right)\left( {2x + 3y} \right)}} = – {{2\left( {1 + x + {x^2}} \right)} \over {2x + 3y}}\)
Câu 38: Rút gọn biểu thức :
a. \({{{x^4} – x{y^3}} \over {2xy + {y^2}}}:{{{x^3} + {x^2}y + x{y^2}} \over {2x + y}}\)
b. \({{5{x^2} – 10xy + 5{y^2}} \over {2{x^2} – 2xy + 2{y^2}}}:{{8x – 8y} \over {10{x^3} + 10{y^3}}}\)
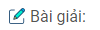
a. \({{{x^4} – x{y^3}} \over {2xy + {y^2}}}:{{{x^3} + {x^2}y + x{y^2}} \over {2x + y}}\)\( = {{{x^4} – x{y^3}} \over {2xy + {y^2}}}.{{2x + y} \over {{x^3} + {x^2}y + x{y^2}}} \)
\(
= {{x\left( {{x^3} – {y^3}} \right)\left( {2x + y} \right)} \over {y\left( {2x + y} \right).x\left( {{x^2} + xy + {y^2}} \right)}}\)
\( = {{\left( {x – y} \right)\left( {{x^2} + xy + {y^2}} \right)} \over {y\left( {{x^2} + xy + {y^2}} \right)}} = {{x – y} \over y}\)
b. \({{5{x^2} – 10xy + 5{y^2}} \over {2{x^2} – 2xy + 2{y^2}}}:{{8x – 8y} \over {10{x^3} + 10{y^3}}}\)\( = {{5{x^2} – 10xy + 5{y^2}} \over {2{x^2} – 2xy + 2{y^2}}}.{{10{x^3} + 10{y^3}} \over {8x – 8y}}\)
\(
= {{5\left( {{x^2} – 2xy + {y^2}} \right).10\left( {{x^3} + {y^3}} \right)} \over {2\left( {{x^2} – xy + {y^2}} \right).8\left( {x – y} \right)}}\)
\( = {{25{{\left( {x – y} \right)}^2}\left( {x + y} \right)\left( {{x^2} – xy + {y^2}} \right)} \over {8\left( {{x^2} – xy + {y^2}} \right)\left( {x – y} \right)}} \)
\(
= {{25\left( {x – y} \right)\left( {x + y} \right)} \over 8}\)
Câu 39: Thực hiện phép chia phân thức :
a. \({{{x^2} – 5x + 6} \over {{x^2} + 7x + 12}}:{{{x^2} – 4x + 4} \over {{x^2} + 3x}}\)
b. \({{{x^2} + 2x – 3} \over {{x^2} + 3x – 10}}:{{{x^2} + 7x + 12} \over {{x^2} – 9x + 14}}\)
a. \({{{x^2} – 5x + 6} \over {{x^2} + 7x + 12}}:{{{x^2} – 4x + 4} \over {{x^2} + 3x}}\)\( = {{{x^2} – 5x + 6} \over {{x^2} + 7x + 12}}.{{{x^2} + 3x} \over {{x^2} – 4x + 4}}\)
\( = {{\left( {{x^2} – 5x + 6} \right).x\left( {x + 3} \right)} \over {\left( {{x^2} + 7x + 12} \right){{\left( {x – 2} \right)}^2}}} = {{\left( {{x^2} – 2x – 3x + 6} \right).x\left( {x + 3} \right)} \over {\left( {{x^2} + 3x + 4x + 12} \right){{\left( {x – 2} \right)}^2}}}\)
\( = {{\left[ {x\left( {x – 2} \right) – 3\left( {x – 2} \right)} \right].x\left( {x + 3} \right)} \over {\left[ {x\left( {x + 3} \right) + 4\left( {x + 3} \right)} \right]{{\left( {x – 2} \right)}^2}}}\)
\( = {{x\left( {x – 2} \right)\left( {x – 3} \right)\left( {x + 3} \right)} \over {\left( {x + 3} \right)\left( {x + 4} \right){{\left( {x – 2} \right)}^2}}} = {{x\left( {x – 3} \right)} \over {\left( {x + 4} \right)\left( {x – 2} \right)}}\)