Câu hỏi khởi động
Số Pi được người Ba-bi-lon(Babylon) cổ đại phát hiện gần bốn nghìn năm trước và được biểu diễn bằng chữ cái Hy Lạp \(\pi\) từ giữa thế kỉ XVIII. Số \(\pi\) thể hiện mối liên hệ đặc biệt giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó. Mối liên hệ đặc biệt giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó là gì?

Độ dài đường tròn= Chu vi đường tròn= \(\pi.d\), với d là đường kính của đường tròn đó

Tỉ lệ giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó là:
\(\pi.d : d\)= \(\pi\)
Vậy tỉ lệ độ dài của một đường tròn với độ dài đường kính của đường tròn đó luôn bằng \(\pi\)
Luyện tập vận dụng 1

a) Viết tỉ số của: -5 và -7; 23,7 và 89,6; 4 và \(\frac{3}{7}\)
b) Trong các tỉ số đã viết, tỉ số nào là phân số?

Tỉ số của số a và số b phải được viết theo đúng thứ tự là \(\frac{a}{b}\) hoặc a : b.

a) \(\frac{{ – 5}}{{ – 7}}\); \(\frac{{23,7}}{{89,6}}\); \(4:\frac{3}{7}\)
b) Trong các tỉ số trên có \(\frac{-5}{-7}\) là phân số.
Luyện tập vận dụng 2

Trong không khí, ánh sáng chuyến động với vận tốc khoảng 300 000 km/s, còn âm thanh lan truyền với vận tốc khoảng 343,2 m/s. (Nguồn: https://vi.wikipedia.org)
Tính tỉ số của vận tốc ánh sáng và vận tốc âm thanh.

Tỉ số của số a và số b phải được viết theo đúng thứ tự là \(\frac{a}{b}\) hoặc a : b.

Ta có: Vận tốc chuyển động của ánh sáng là: \(300{\rm{ }}000{\rm{ }}km/s = 300{\rm{ }}000{\rm{ }}000{\rm{ }}m/s\)
Vận tốc chuyển động của ánh sáng là: \(343,2{\rm{ }}m/s\)
Vậy tỉ số của vận tốc ánh sáng và vận tốc âm thanh là: \(\frac{{300{\rm{ }}000{\rm{ }}000}}{{343,2}}\)
Hoạt động 3

Tính tỉ số phần trăm của 3 và 5.

Tỉ số phần trăm của a và b là \(\frac{a}{b}.100\% \)

Tỉ số phần trăm của 3 và 5 là:
\(\frac{3}{5}.100\% = 60\% \)
Luyện tập vận dụng 3

Tính tỉ số phần trăm của a và b với b lần lượt là các số sau: 10; 100; 1 000.

Tỉ số phần trăm của a và b là \(\frac{a}{b}.100\% \)

Tỉ số phần trăm của a và b với b = 10 là: \(\frac{a}{{10}}.100\% = 10a\% \)
Tỉ số phần trăm của a và b với b = 100 là: \(\frac{a}{{100}}.100\% = a\% \)
Tỉ số phần trăm của a và b với b = 1000 là: \(\frac{a}{{1000}}.100\% = \frac{a}{{10}}\% \)
Luyện tập vận dụng 4

Tính tỉ số phần trăm (làm tròn đến hàng phần mười) của 12 và 35.

Khi tính tỉ số phần trăm của a và b mà phải làm tròn số thập phân thì ta làm theo cách thứ hai đã nêu ở trên: Nhân a với 100 rồi chia cho b và làm tròn số thập phân nhận được.

Tỉ số phần trăm của 12 và 35 là:
Advertisements (Quảng cáo)
\(\frac{{12.100}}{{35}}\% \approx 34,3\% \)
Hoạt động 4

Xe ô tô tải đi với vận tốc 45 km/h, xe ô tô con đi với vận tốc 60 km/h.
Vận tốc của xe ô tô tải bằng bao nhiêu phần trăm vận tốc của xe ô tô con?

Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là: \(\frac{{a.100}}{b}\% \)

Tỉ số vận tốc của xe ô tô tải và xe ô tô con là: \(\frac{{45.100}}{{60}}\% = 75\% \).
Luyện tập vận dụng 5

Theo http://vietnam.unfpa.org ngày 19/12/2017, dân số Việt Nam tính đến 0 giờ ngày 01/4/2019 là 96 208 984 người, trong đó có 47 881 061 nam và 48 327 923 nữ. Hãy tính tỉ số phần trăm của dân số nữ so với dân số cả nước (làm tròn đến hàng phần trăm).

Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là: \(\frac{{a.100}}{b}\% \)

Tỉ số phần trăm của dân số nữ so với dân số cả nước là:
\(\frac{{48{\rm{ }}327{\rm{ }}923}}{{96{\rm{ }}208{\rm{ }}984}}\% = 50,2\% \)
Giải bài 1 trang 65 Toán 6 tập 2 Cánh diều

Tính tỉ số của:
a) \(\frac{4}{3}m\) và \(75\,cm\)
b) \(\frac{7}{{10}}\) giờ và \(25\) phút
c) \(10\,\,kg\) và \(10\) tạ.

Tỉ số của số a và số b phải được viết theo đúng thứ tự là \(\frac{a}{b}\) hoặc a : b.
Chú ý: Đưa các đại lượng về cùng đơn vị đo.

a) Đổi \(75\,cm = \frac{{75}}{{100}} = \frac{3}{4}\) m
=> Tỉ số: \(\frac{4}{3}:\frac{3}{4} = \frac{{16}}{9}\).
b) Đổi 25 phút = \(\frac{{25}}{{60}} = \frac{5}{{12}}\) giờ
=> Tỉ số: \(\frac{7}{{10}}:\frac{5}{{12}} = \frac{{42}}{{25}}\)
c) Đổi 10 tạ = 1000 kg
Advertisements (Quảng cáo)
=> Tỉ số: \(10:1000 = \frac{1}{{100}}\)
Giải bài 2 trang 65 Toán 6 tập 2 Cánh diều

Tính tỉ số phần trăm (làm tròn đến hàng phần mười) của:
a) 16 và 75;
b) 6,55 và 8,1.

Tỉ số phần trăm của a và b là \(\frac{a}{b}.100\% \).

a) Tỉ số phần trăm của 16 và 75 là:
\(\frac{{16}}{{75}}.100\% = 21,3\% \)
b) Tỉ số phần trăm của 6,55 và 8,1 là:
\(\frac{{6,55}}{{8,1}}.100\% = 80,9\% \)
Giải bài 3 trang 65 Toán 6 Cánh diều

Một doanh nghiệp thống kê số lượng xi măng bán được trong bốn tháng cuối năm 2019 ở biểu
đồ trong Hình 1.
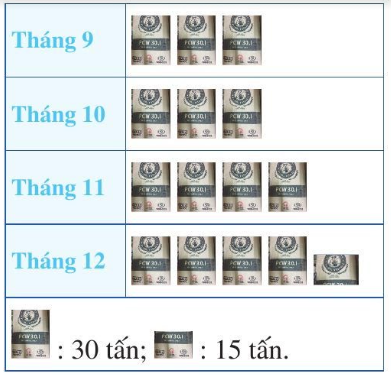
a) Hỏi tháng nào doanh nghiệp bán được nhiều xi măng nhất? Ít xi măng nhất?
b) Tính tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng (làm tròn kết quả đến hàng đơn vị).

a) Quan sát biểu đồ để xác định tháng nào doanh nghiệp bán được nhiều xi măng nhất? Ít xi măng nhất?
b) – Tính số lượng xi măng bán ra trong tháng 12
– Tính tổng số lượng xi măng bán ra trong cả bốn tháng.
=> Tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng.

a) Tháng 12 doanh nghiệp bán được nhiều xi măng nhất
Tháng 9 và tháng 10 doanh nghiệp bán được ít xi măng nhất
b)
Lượng xi măng bán ra trong tháng 12 là: \(30.4 + 15 = 135\)(tấn)
Tổng lượng xi măng bán ra trong cả bốn tháng là:
\(3.30 + 3.30 + 4.30 + 135 = 435\) (tấn).
Tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng lượng xi măng bán ra trong cả bốn tháng là:
\(\frac{{135}}{{435}}.100\% = 31\% \)
Bài 4 trang 66 Toán 6 tập 2 Cánh diều

Biểu đồ ở Hình 2 thống kê số giờ đọc sách của bạn Châu trong ba ngày cuối tuần.
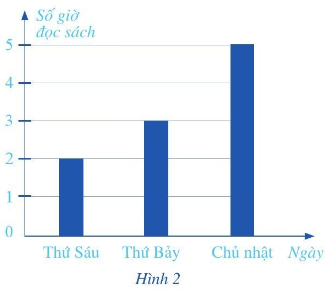
a) Bạn Châu đọc sách nhiều nhất vào ngày nào?
b) Tính tỉ số phần trăm (làm tròn đến hàng phần mười) của tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần so với tổng số giờ trong ba ngày cuối tuần.
Theo em, bạn Châu có nên dành nhiều thời gian để đọc sách hơn không?

a) Châu đọc sách nhiều nhất vào ngày có cột số giờ đọc sách cao nhất.
b)
– Tính tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần
– Tính tổng số giờ trong ba ngày cuối tuần
=> Tỉ số phần trăm của tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần so với tổng số giờ trong ba ngày cuối tuần

a) Bạn Châu đọc sách nhiều nhất vào ngày chủ nhật
b)
Tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần là: \(2 + 3 + 5 = 10\) giờ.
Tổng số giờ trong ba ngày cuối tuần là: \(24.3 = 72\)
Tỉ số phần trăm của tổng số giờ đọc sách của bạn Châu trong ba ngày cuối tuần so với tổng số giờ trong ba ngày cuối tuần là:
\(\frac{{10}}{{72}}.100\% = 13,9\% \)
Vậy bạn Châu nên dành nhiều thời gian để đọc sách hơn.
Giải bài 5 trang 66 Toán 6 Cánh diều tập 2

Xếp loại thi đua ba tổ lao động của một đội sản xuất được thống kê như sau:
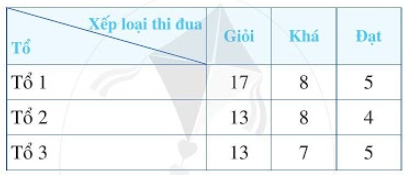
a) Mỗi tổ lao động có bao nhiêu người?
b) Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội là lớn hơn 53%. Thông báo đó của đội trưởng có đúng không?

a) Số lao động mỗi tổ = Số lao động giỏi + số lao động khá + số lao động đạt (của mỗi tổ)
b)
– Tính số lao động giỏi ở cả đội.
– Tính số người ở cả đội.
=> Tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội.

a) Tổ 1 có 17 + 8 + 5 = 30 người
Tổ 2 có 13 + 8 + 4 = 25 người
Tổ 3 có 13 + 7 + 5 = 25 người.
b) Số lao động giỏi ở cả đội là: \(17 + 13 + 23 = 43\) người
Số người ở cả đội là: \(30 + 25 + 25 = 80\) người.
Tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội là:
\(\frac{{43}}{{80}}.100\% = 53,75\% \)
=> Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi ở cá đội so với số người ở cả đội là lớn hơn 53% là đúng.

