Bài 25.18: Trong một thí nghiệm Y-âng, hai khe F1, F2 cách nhau 1,2 mm và cách màn quan sát 0,8 m. Bước sóng của ánh sáng là 546 nm.
a) Tính khoảng vân.
b) Tại hai điếm M1 ,M2 lần lượt cách vân chính giữa 1,07 mm và 0,91 mm có vân sáng hay vân tối thứ mấy, kể từ vân chính giữa ?
a) Theo bài ra ta có \(i = {{\lambda D} \over a} = {{{{546.10}^{ – 6}}.0,{{8.10}^{ – 3}}} \over {1,2}} = {364.10^{ – 3}}mm\)
b) Tại \({M_1}\,:x = 1,07mm = {{1,07} \over {0,364}}i = 3i\)
Vậy tại M1 có vân sáng thứ 3
Tại \({x_2} = 0,91mm = {{0,91} \over {0,364}}i = 2,5i = \left( {3 – {1 \over 2}} \right)i\)
Vậy tại M2 có vân tối thứ 3
Bài 25.19: Một người dự định làm thí nghiệm Y-âng với bức xạ vàng \(\lambda\) = 0,59 \(\mu\)m của natri. Người ấy đặt màn quan sát cách mặt phẳng của hai khe một khoảng D = 0,6 m và dự định thu được một hệ vân có khoảng vân i = 0,4 mm.
a) Hỏi phải chế tạo hai khe F1, F2 cách nhau bao nhiêu ?
b) Sau khi làm được hai khe và tiến hành thí nghiệm, người ấy quan sát được 7 vân sáng nhưng khoảng cách giữa hai vân ngoài cùng chỉ đo được 2,1 mm. Hỏi khoảng cách đúng của hai khe F1, F2 là bao nhiêu ?
Khoảng cách dự kiến \(a_0\) của hai khe :
\({a_0} = {{\lambda D} \over i} = {{0,{{59.10}^{ – 3}}.0,{{6.10}^3}} \over {0,4}} = 0,885\,mm\)
b) Khoảng cách thực của hai khe
\(a = {{0,59.0,6} \over {{{2,1} \over 6}}} = {{0,59.0,6.6} \over {2,1}} = 1mm\)
Bài 25.20: Một tấm nhôm mỏng, trên có rạch hai khe hẹp song song F1, F2, đặt trước một màn M, cách một khoảng D = 1,2 m. Đặt giữa màn và hai khe một thấu kính hội tụ, người ta tìm được hai vị trí của thấu kính, cách nhau một khoảng d = 72 cm cho ta ảnh rõ nét của hai khe trên màn. Ở vị trí mà ảnh lớn hơn thì khoảng cách giữa hai ảnh F1, F2 là 3,8 mm. Bỏ thấu kính đi rồi chiếu sáng hai khe bằng một nguồn điểm S phát ánh sáng đơn sắc bước sóng \(\lambda\) = 656 nm. Tính khoảng cách i giữa hai vân giao thoa trên màn
Gọi d1, d’1 và d2, d’2 lần lượt là các khoảng cách từ hai khe đến thấu kính và từ thấu kính đến màn ở hai vị trí của thấu kính. Ta có :
d1 +d’1 = d2+d’2 = D = 1,2 m = 120 cm và d2 – d1 =72 cm.
Theo tính chất trở lại ngược chiều của ánh sáng, ta biết rằng : d’1 =d2và d’2 = d1
Do đó : d’1 – d1 = d2 – d’2 = d = 72 cm.
Ở một trong hai vị trí của thấu kính thì ảnh lớn hơn vật, còn ở vị trí kia thì ảnh nhỏ hom. Mà ảnh lớn hơn vật khi d’ > d. Vậy, ở vị trí thứ nhất thì ảnh lớn hơn và ta có :
d’1 – d1 =72 ; 2d’1 = 120 + 72 ⟹ d’1; = 96 cm
d1 = 120 – 96 = 24 cm và \(k = \left| {{{d{‘_1}} \over {{d_1}}}} \right|\)
Khoảng cách giữa hai khe là :
\(\eqalign{
& a = {F_1}{F_2} = {{F{‘_1}F{‘_2}} \over 4} = {{3,8} \over 4} = 0,95mm \cr
& i = {{\lambda D} \over a} = {{{{656.10}^{ – 6}}.1,{{2.10}^{ – 3}}} \over {0,95}} = 0,83mm \cr} \)
Bài 25.21: Trong một thí nghiệm Y-âng, hai khe F1, F2 cách nhau một khoảng a = 1,8 mm. Hệ vân được quan sát qua một kính lúp, trong đó có một thước đo cho phép ta đo các khoảng vân chính xác tới 0,01 mm (gọi là thị kính trắc vi). Ban đầu, người ta đo được 16 khoảng vân và được giá trị 2,4 mm. Dịch chuyển kính lúp ra xa thêm 30 cm cho khoảng vân rộng thêm thì đo được 12 khoảng vân và được giá trị 2,88 mm. Tính bước sóng của bức xạ.
Gọi D là khoảng cách từ màn mang hai khe F1, F2 đến mặt phẳng tiêu vật của kính lúp, ở vị trí thứ nhất, và D + 30 là khoảng cách ở vị trí thứ hai. Ta có hai phương trình :
\(\eqalign{
& i = {{2,4} \over {16}} = {{\lambda D} \over a} = {{\lambda D} \over {1,8}} \cr
& i’ = {{2,88} \over {12}} = {{\lambda \left( {D + 30} \right)} \over a} \cr} \)
Advertisements (Quảng cáo)
Giải ra ta được : D = 50 cm và \(\lambda\) = 0,54 \(\mu\)m.
Bài 25.22: Trong một thí nghiệm Y-âng, khoảng cách a giữa hai khe F1, F2 là 2 mm, khoảng cách D từ F1, F2 tới màn quan sát là 1,2 m. Nguồn điểm phát đồng thời hai bức xạ đơn sắc, bước sóng lần lượt là \(\lambda_1\) = 660 nm và \(\lambda_2\) = 550 nm.
a) Tính khoảng cách \(i_1\) giữa hai vân sáng màu đỏ (\(\lambda_1\) ) và khoảng cách \(i_2\) giữa hai vân sáng màu lục (\(\lambda_2\) ).
b) Tính khoảng cách từ vân chính giữa đến vân sáng đầu tiên trên màn cùng màu với nó.
Với bức xạ đỏ, \(\lambda_1\)= 660 nm = 0,66 \(\mu\)m
\(i_1\)=0,396mm
Với bức xạ lục – vàng, \(\lambda_2\) = 550 nm = 0,55 \(\mu\)m
\(i_2\)=0,33mm
b) Vân chính giữa ứng với k = 0 là chung cho cả hai bức xạ, tức là tại đó cả hai bức xạ cùng cho vân sáng và vân có màu là màu hỗn hợp của màu đỏ và màu lục, tức là màu vàng – da cam.
Vân đầu tiên cùng màu với vân này ở tại điểm A cách tâm O của vân chính giữa một khoảng X = OA sao cho :x=i1k1= i2k2 hay là 0,396k1 = 0,33k2 ;
với k1 , k2 là hai số nguyên.
Ta nhận thấy : 6k1 = 5k2 .
Vậy giá trị nhỏ nhất của k1 là 5 và của k2 là 6, tức là :
OA = 0,396.5 = 0,33.6 = 1,98 mm
Bài 25.23: Một nguồn sáng điểm phát đồng thời một bức xạ đơn sắc màu đỏ, bước sóng \(\lambda_1\)= 640 nm và một bức xạ màu lục, chiếu sáng hai khe Y-âng. Trên màn quan sát, người ta thấy giữa hai vân sáng cùng màu với vân chính giữa có 7 vân màu lục. Hỏi :
– Giữa hai vân sáng nói trên có bao nhiêu vân màu đỏ ?
– Bước sóng của bức xạ màu lục là bao nhiêu ?
Giữa hai vân sáng cùng màu với vân chính giữa có 7 vân sáng màu lục, giữa 7 vân màu lục này có 6 khoảng vân màu lục cộng thêm hai khoảng nữa từ hai vân ở hai đầu đến hai vân trùng với vân màu đỏ.
Vậy, có tất cả 6 + 2 = 8 khoảng vân màu lục \(i_l\)
Giữa hai vân sáng cùng màu với vân chính giữa lại có một số nguyên lần khoảng vân \(i_đ\) màu đỏ, tức là ta có : 8\(i_l\)
Advertisements (Quảng cáo)
= k\(i_đ\)
k phải là một số nguyên và nguyên tố cùng số 8.
Mà iđlại lớn hơn \(i_l\) nên k chỉ có thể là 3, 5 hoặc 7.
k = 3. Ta có 8il = 3iđ hay là 8\(\lambda_l\) = 3\(\lambda_đ\) (vì ỉ tỉ lệ thuận với \(\lambda\)).
Do đó :\(\lambda_l\) =\(3\over 8\)\(\lambda_đ\) = \(3\over8\)640 = 240 nm.
Bức xạ này ở trong miền tử ngoại (loại).
k = 5 Làm tương tự ta cũng được :
\(\lambda_l\) =\(5\over8\)\(\lambda_đ\) = \(5\over8\)640 = 400 nm.
Bức xạ này có màu tím nên cũng không chấp nhận được.
k = 7 :\(\lambda_l\) =\(7\over8\)\(\lambda_đ\) = \(7\over8\)640 = 560 nm.
Bức xạ này đúng là có màu lục. Vậy :
– Giữa hai vân sáng nói trên có 7 – 1 vân màu đỏ.
– Bước sóng của bức xạ lục là 560 nm.
Bài 25.24: Trong một thí nghiệm Y-âng, khoảng cách giữa hai khe F1, F2 là 1,2 mm, các vân được quan sát qua một kính lúp, tiêu cự f = 4 cm, đặt cách mặt phẳng của hai khe một khoảng L = 40 cm. Trong kính lúp người ta đếm được 15vân sáng. Khoảng cách giữa tâm của hai vân sáng ngoài cùng đo được là 2,1 mm.
a) Tính góc trông khoảng vân i và bước sóng của bức xạ.
b) Nếu đặt toàn bộ dụng cụ trong nước, có chiết suất n = \(4\over3\) thì khỏang cách giữa hai vân nói trên sẽ là bao nhiêu ?
a) Khi quan sát vân bằng kính lúp thì ta trông thấy ảnh của hệ vân nằm trên mặt phẳng tiêu vật của kính lúp và ảnh đó ở xa vô cùng (H.25.1G).
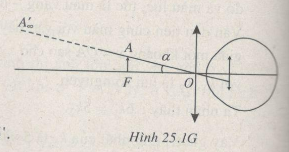
Ta thấy \(\alpha = tan \alpha = {i\over f}= 12,5’\)
Khoảng cách từ hai khe tới mặt phẳng của các vân : D = L – f = 40 – 4 = 36 cm = 0,36 m.
Bước sóng của bức xạ là :
\(\lambda = {{ia} \over D} = {{2,1.1,2} \over {1,4.0,{{36.10}^3}}} = 0,{5.10^{ – 3}}mm\)
b) Trong môi trường chiết suất n, tốc độ ánh sáng giảm n lần nhưng tần số không đổi, do đó bước sóng và khoảng vân i giảm n lần.
Ta có : \(\lambda ‘ = {\lambda \over n} = {\lambda \over {{4 \over 3}}} = {3 \over 4}\lambda = {3 \over 4}.0,5 = 0,{375.10^{ – 3}}mm\) và khoảng cách giữa hai vân nói trên thành 1,575 mm
Bài 25.25: Một khe hẹp F phát ánh sáng trắng chiếu sáng hai khe song song F1, F2 cách nhau 1,5 mm. Màn M quan sát vân giao thoa cách mặt phảng của hai khe một khoảng D = 1,2 m.
a) Tính các khoảng vân i1 và i2 cho bởi hai bức xạ giới hạn 750 nm và 400 nm của phổ khả kiến.
b) Ở điểm A trên màn M, cách vân chính giữa 2 mm có vân sáng của những bức xạ nào và vân tối của những bức xạ nào ?
a) Với \(\lambda_1\)= 750 nm = 0,75 \(\mu\)m thì \(i_1\) = 0,6 mm.
Với \(\lambda_2\) = 400 nm = 0,40 \(\mu\)m thì i2 = 0,32 mm.
b) Đặt X = OM = ki=\(k{{\lambda D} \over a}\) thì bức xạ nào ứng với k nguyên sẽ cho vân sáng, bức xạ ứng với k nửa nguyên cho vâri tối.
Do \(\lambda\) chỉ ở trong khoảng 400 nm và 750 nm, nên khoảng vân i lớn nhất cũng chì bằng i1 và nhỏ nhất cũng chỉ bằng ỉ2 nên k phải ở trong khoảns k1 và k2 xấc định bởi :
x = k1i1 = k2i2 hay là 2 = 0,6k1 = 0,32k2
tức là k1 = 2: 0,6 = 3,3 … và k2 = 2:0,32 = 6,25. Như vây 3,3 < k < 6,25.
Từ 3,3 đến 6,25 có ba số nguyên : 4, 5, 6 và có ba số nửa nguyên 3,5 ; 4,5 và 5,5.
Vậy, có ba bức xạ cho vân sáng, bước sóng lần lượt là :
\(\lambda_1\)= 625 nm ;\(\lambda_2\) = 500 nm ; \(\lambda_3\)= 417 nm.
Và cũng có ba bức xạ cho vân tối, bước sóng lần lượt :
\(\lambda_1\)’=714nm; \(\lambda_2\)’=556nm ; \(\lambda_3\)’=455nm
Bài 25.26: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu sáng bằng ánh sáng đơn sắc có bước sóng 0,6 \(\mu\)m. Khoảng cách giữa hai khe là 1 mm. Khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2,5 m. Bề rộng miền giao thoa là 1,25 cm. Tính tổng số vân sáng’và vân tối trong miền giao thoa.
Khoảng vân giao thoa :
\(i = {{\lambda D} \over a} = {{0,{{6.10}^{ – 6}}.2,5} \over {{{10}^{ – 3}}}} = 1,{5.10^{ – 3}}m = 1,5mm\)
Số khoảng vân trong một nửa bề rộng của miền giao thoa :
\(N = {L \over {2i}} = {{2,5} \over {2.1,5}} = 4,17\)
Số vân sáng trong một nửa bề rộng, không kể vân trung tâm là 4 vân. Số vân sáng trong cả bề rộng của miền giao thoa, kể cả vân trung tâm :
(2.4) + 1 = 9 vân
Số vân tối trong một nửa bề rộng : 4 vân.
Số vân tối trong cả bề rộng của miền giao thoa : 2. 4 = 8 vân.
Tổng số vân sáng và vân tối trong miền giao thoa : 9 + 8 = 17 vân.
