Bài 23: Tìm nghiệm phức phương trình \(z + {1 \over z} = k\) trong các trường hợp sau:
a) \(k = 1\);
b) \(k = \sqrt 2 \)
c) \(k = 2i\)
Giải
\(z + {1 \over z} = k\)
Ta có \(z + {1 \over z} = k \Leftrightarrow {z^2} – kz + 1 = 0\)
Phương trình có hai nghiệm là \(z = {{k \pm \delta } \over 2}\) trong đó \(\delta \) là một căn bậc hai của \(\Delta = {k^2} – 4\)
a) Với \(k = 1\) thì \(\Delta = – 3\) khi đó \(z = {{1 \pm \sqrt 3 i} \over 2}\)
b) Với \(k = \sqrt 2 \) thì \(\Delta = – 2\) khi đó \(z = {{\sqrt 2 \pm \sqrt 2 i} \over 2}\)\( = {{\sqrt 2 } \over 2}\left( {1 \pm i} \right)\)
c) Với \(k = 2i\) thì \(\Delta = – 8\) khi đó \(z = {{2i \pm 2\sqrt 2 i} \over 2} = \left( {1 \pm \sqrt 2 } \right)i\)
Bài 24: Giải các phương trình sau trên C và biểu diễn hình hợp tập hợp các nghiệm của mỗi phương trình (trong mặt phẳng phức):
a)\({z^3} + 1 = 0\);
b) \({z^4} – 1 = 0\);
c) \({z^4} + 4 = 0\);
d) \(8{z^4} + 8{z^3} = z + 1\).
Giải
a) \({z^3} + 1 = 0 \Leftrightarrow \left( {z + 1} \right)\left( {{z^2} – z + 1} \right) = 0\)
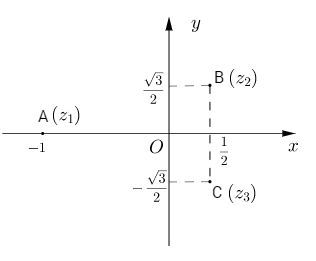
Nghiệm của \(z + 1 = 0\) là \({z_1} = – 1\)
\({z^2} – z + 1 = 0 \Leftrightarrow {\left( {z – {1 \over 2}} \right)^2} = – {3 \over 4} = {\left( {{{\sqrt 3 } \over 2}i} \right)^2}\)
\( \Leftrightarrow \left[ \matrix{ z = {1 \over 2} + {{\sqrt 3 } \over 2}i = {z_2} \hfill \cr z = {1 \over 2} – {{\sqrt 3 } \over 2}i = {z_3} \hfill \cr} \right.\)
Vậy \(S = \left\{ { – 1;{1 \over 2} + {{\sqrt 3 } \over 2}i;{1 \over 2} – {{\sqrt 3 } \over 2}i} \right\}\)
Advertisements (Quảng cáo)
b) \({z^4} – 1 = 0 \Leftrightarrow \left( {{z^2} – 1} \right)\left( {{z^2} + 1} \right) = 0\)
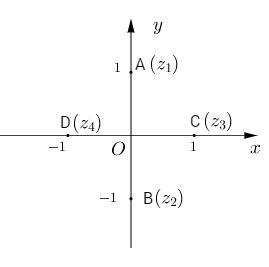
\( \Leftrightarrow \left[ \matrix{ {z^2} – 1 = 0 \hfill \cr {z^2} + 1 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ z = \pm 1 \hfill \cr z = \pm i \hfill \cr} \right.\)
Phương trình có 4 nghiệm \({z_1} = i,{z_2} = – i,{z_3} = 1,{z_4} = – 1\)
c) \({z^4} + 4 = 0 \Leftrightarrow \left( {{z^2} + 2i} \right)\left( {{z^2} – 2i} \right) = 0\)
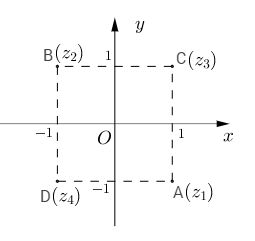
Nghiệm của \({z^2} + 2i = 0\) là các căn bậc hai của -2i, đó là \({z_1} = 1 – i\),\({z_2} = – 1 + i\)
Nghiệm của \({z^2} – 2i = 0\) là các căn bậc hai của 2i, đó là \({z_3} = 1 + i\),\({z_4} = – 1 – i\)
Vậy \({z^4} + 4 = 0\) có bốn nghiệm \({z_1},{z_2},{z_3},{z_4}\).
d) \(8{z^4} + 8{z^3} = z + 1 \Leftrightarrow \left( {z + 1} \right)\left( {8{z^3} – 1} \right) = 0\)
\( \Leftrightarrow \left( {z + 1} \right)\left( {2z – 1} \right)\left( {4{z^2} + 2z + 1} \right) = 0\)
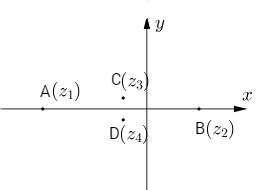
Nghiệm của \(z + 1 = 0\) là \({z_1} = – 1\)
Nghiệm của \(2z – 1 = 0\) là \({z_2} = {1 \over 2}\)
Nghiệm của \(4{z^2} + 2z + 1 = 0\) hay \({\left( {2z + {1 \over 2}} \right)^2} + {3 \over 4} = 0\)là \({z_3} = – {1 \over 4} + {{\sqrt 3 } \over 4}i\) và\({z_4} = – {1 \over 4} – {{\sqrt 3 } \over 4}i\)
Vậy phương trình đã cho có bốn nghiệm\({z_1},{z_2},{z_3},{z_4}\)
Advertisements (Quảng cáo)
Bài 25: a) Tìm các số thực b, c để phương trình (với ẩn z):
\({z^2} + bz + c = 0\)
nhận \(z = 1 + i\) làm một nghiệm.
b) Tìm các số thực a, b, c để phương trình (với ẩn z):
\({z^3} + a{z^2} + bz + c = 0\)
nhận \(z = 1 + i\) làm nghiệm và cũng nhận \(z = 2\) là nghiệm.
Giải
a) \(1 + i\) là một nghiệm của phương trình \({z^2} + bz + c = 0\) khi và chỉ khi
\({\left( {1 + i} \right)^2} + b\left( {1 + i} \right) + c = 0 \Leftrightarrow 2i + b + bi + c = 0\)
\( \Leftrightarrow b + c + \left( {2 + b} \right)i = 0\)
\(\Leftrightarrow \left\{ \matrix{ b + c = 0 \hfill \cr 2 + b = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ b = – 2 \hfill \cr c = 2 \hfill \cr} \right.\)
b) \(1 + i\) là một nghiệm của \({z^3} + a{z^2} + bz + c = 0\) khi và chỉ khi
\({\left( {1 + i} \right)^3} + a{\left( {1 + i} \right)^2} + b\left( {1 + i} \right) + c = 0 \)
\(\Leftrightarrow \left( {b + c – 2} \right)+\left( {2 + 2a + b} \right)i = 0\)
\( \Leftrightarrow \left\{ \matrix{ b + c – 2 = 0\,\,\,\,\,\,\,\,\left( 1 \right) \hfill \cr 2a + b + 2 = 0\,\,\,\,\,\left( 2 \right) \hfill \cr} \right.\)
\(2\) là nghiệm của \({z^3} + a{z^2} + bz + c = 0\) khi và chỉ khi \(8 + 4a + 2b + c = 0\,\,\,\left( 3 \right)\)
Từ (1), (2), (3) ta có hệ: .\(\left\{ \matrix{ b + c = 2 \hfill \cr 2a + b = – 2 \hfill \cr 4a + 2b + c = – 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = – 4 \hfill \cr b = 6 \hfill \cr c = – 4 \hfill \cr} \right.\)
Bài 26: a) Dùng công thức cộng trong lượng giác để chứng minh rằng với mọi số thực \(\varphi \), ta có \({\left( {\cos \varphi + i\sin \varphi } \right)^2} = \cos 2\varphi + i\sin 2\varphi \).
Từ đó hãy tìm mọi căn bậc hai của số phức \(\cos 2\varphi + i\sin 2\varphi \). Hãy so sánh cách giải này với cách giải trong bài học ở bài 2.
b) Tìm các căn bậc hai của \({{\sqrt 2 } \over 2}\left( {1 – i} \right)\) bằng hai cách nói ở câu a).
Giải
a) Với mọi \(\varphi \) ta có: \({\left( {\cos \varphi + i\sin \varphi } \right)^2} = {\cos ^2}\varphi – {\sin ^2}\varphi + \left( {2\sin \varphi \cos \varphi } \right)i\)
\( = \cos 2\varphi + i\sin 2\varphi \)
Vậy các căn bậc hai của \(\cos 2\varphi + i\sin 2\varphi \) là \( \pm \left( {\cos \varphi + i\sin \varphi } \right)\)
Theo cách giải trong bài học, để tìm căn bậc hai của\(\cos 2\varphi + i\sin 2\varphi \) ta giải hệ phương trình\(\left\{ \matrix{ {x^2} – {y^2} = \cos 2\varphi \hfill \cr 2xy = \sin 2\varphi \hfill \cr} \right.\)
Rõ ràng hệ có các nghiệm \(\left( {\cos \varphi ,\sin \varphi } \right),\left( { – \cos \varphi , – \sin \varphi } \right)\) do đó\( \pm \left( {\cos \varphi + i\sin \varphi } \right)\) là hai căn bậc hai của\(\cos 2\varphi + i\sin 2\varphi \). Ta biết rằng chỉ có hai căn như thế nên đó là tất cả các căn bậc hai cần tìm.
b) \({{\sqrt 2 } \over 2}\left( {1 – i} \right) \)
\(= \cos {\pi \over 4} – i\sin {\pi \over 4} = \cos \left( { – {\pi \over 4}} \right) + i\sin \left( { – {\pi \over 4}} \right)\)
\(\text{ thì theo câu a) }, {{\sqrt 2 } \over 2}\left( {1 – i} \right)\) có hai căn bậc hai là \( \pm \left( {\cos \left( {{{ – \pi } \over 8}} \right) + i\sin \left( {{{ – \pi } \over 8}} \right)} \right) = \pm \left( {\cos {\pi \over 8} – i\sin {\pi \over 8}} \right)\)
Mà \(\eqalign{ & \cos {\pi \over 8} = \sqrt {{{1 + \cos {\pi \over 4}} \over 2}} = \sqrt {{{1 + {{\sqrt 2 } \over 2}} \over 2}} \cr& = {1 \over 2}\sqrt {2 + \sqrt 2 } \cr & \sin {\pi \over 8} = \sqrt {{{1 – \cos {\pi \over 4}} \over 2}} = \sqrt {{{1 – {{\sqrt 2 } \over 2}} \over 2}} \cr& = {1 \over 2}\sqrt {2 – \sqrt 2 } \cr} \)
Vậy hai căn bậc hai cần tìm là \( \pm {1 \over 2}\left( {\sqrt {2 + \sqrt 2 } – i\sqrt {2 – \sqrt 2 } } \right)\)
Còn theo bài học, việc tìm các căn bậc hai của\({{\sqrt 2 } \over 2}\left( {1 – i} \right)\) đưa về việc giải hệ phương trình\(\left\{ \matrix{ {x^2} – {y^2} = {{\sqrt 2 } \over 2} \hfill \cr 2xy = – {{\sqrt 2 } \over 2} \hfill \cr} \right.\)
Hệ đó tương đương với \(\left\{ \matrix{ 8{x^4} – 4\sqrt 2 {x^2} – 1 = 0 \hfill \cr y = – {{\sqrt 2 } \over {4x}} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x^2} = {{\sqrt 2 + 2} \over 4} \hfill \cr y = – {{\sqrt 2 } \over {4x}} \hfill \cr} \right.\)
nên có các nghiệm là: \(\left( {{{\sqrt {2 + \sqrt 2 } } \over 2};{{ – \sqrt {2 – \sqrt 2 } } \over 2}} \right),\left( {{{ – \sqrt {2 + \sqrt 2 } } \over 2};{{\sqrt {2 – \sqrt 2 } } \over 2}} \right)\)
Vậy ta lại được hai căn bậc hai đã viết ở trên.

