Câu C1: Sau khi đóng khóa K ít lâu, độ sáng hai bóng đèn Đ1 và Đ2 trên hình 41.1 có giống nhau không? Giải thích tại sao?
Khi đóng khoá K đèn Đ1 sáng lên ngay lập tức, còn đèn Đ2 sáng lên từ từ vì có hiện tượng tự cảm, sau đó ít lâu thì đèn Đ2 cũng sáng lên như đèn Đ1 vì lúc này hiện tượng tự cảm đã chấm dứt.
Câu C2: Hãy thành lập công thức (41.2).
 Sử dụng các còng thức (41.1) và (29.3)
Sử dụng các còng thức (41.1) và (29.3)
Từ công thức (29.3):
\(B = 4\pi {.10^{ – 7}}nI\) (với \(n = {N \over l}\) : số vòng dây trên 1 mét chiều dài ống dây).
Công thức (41.1): \(\phi = LI\)
Ta có: \( \phi= {\rm N}{\rm B}S \Rightarrow \phi = lnBS \)
\(= 4\pi .1{0^{ – 7}}{n^2}SIl = 4\pi .1{0^{ – 7}}{n^2}VI = LI\)
\( \Rightarrow L = 4\pi {.10^{ – 7}}{n^2}V\) với \(V = S.l\)
Câu C3: Có thể áp dụng công thức (41.2) cho ống dây ở hình 41.3a, hay ống dây ở Hình 41.3b SGK, hoặc cả hai ống dây được không?
Công thức \(L = 4\pi {.10^{ – 7}}{n^2}V\) chỉ dùng áp dụng cho ống dây không có lõi sắt, lúc đó L là đại lượng không đổi.
Khi ống dây có lõi sắt thì L tăng lên rất nhiều lần và L được đo bằng thực nghiệm.
Advertisements (Quảng cáo)
Bài 1: Chọn phương án đúng
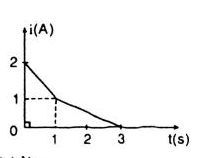
Sự biến đổi của dòng điện trong một mạch điện theo thời gian được cho trên hình 41.4. Gọi suất điện động tự cảm trong khoảng thời gian từ 0s đến 1s là e1, từ 1s đến 3s là e2. Ta có:
A. e1=e2 B. e1=2e2
C. e1=3e2 D. \({e_1} = {1 \over 2}{e_2}\)
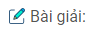
B là phương án đúng.
Suất điện động tự cảm t1 = 0 đến t2 = 1 (s) là
\({e_1} = – L{{\Delta i} \over {\Delta t}} = – L{{1 – 2} \over 1} = L\) (V)
Suất điện động tự cảm từ t2 = 1 (s) đến t3= 3 (s) là:
Advertisements (Quảng cáo)
\({e_2} = – L{{\Delta i} \over {\Delta t}} = – L{{0 – 1} \over 2} = {L \over 2}\)
Vậy e1 = 2e2
Bài 2: Tính hệ sô tự cảm của một ống dây dài 50cm, diện tích tiết diện ngang của ống là 10cm2. Cho biết ống dây có 1000 vòng dây.
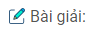
\(l\) = 50cm
S = 10 cm2
N = 1000 vòng
\(V=S.l=10.50=500\) cm3
Ta có hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ – 7}}{n^2}V = 4\pi {.10^{ – 7}}{\left( {{N \over l}} \right)^2}V\)
\(L = 4\pi {.10^{ – 7}}{\left( {{{1000} \over {0,5}}} \right)^2}{.500.10^{ – 6}} \Rightarrow L = 0,25{.10^{ – 2}}\left( H \right)\)
Hay L = 2,5 (mH)
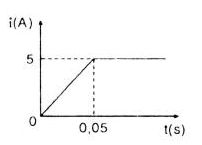
Bài 3: Một ống dây dài được quấn với mật độ 2000 vòng/m. Ống có thể tích 500cm3. Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc, dòng điện trong ống biến đổi theo thời gian như đồ thị trên hình 41.5. lúc đóng công tắc ứng với thời điểm t = 0. Tính suất điện động tự cảm trong ống.
a) Từ sau khi đóng công tắc đến thời điểm t = 0,05s.
b) Tử thời điểm t = 0,05s về sau.
Giải
n = 2000 = 2.103 vòng/m
V = 500cm3 = 5.10-4 m3
Hệ số tự cảm của ống dây:
\(L = 4\pi {.10^{ – 7}}{n^2}V = 4\pi {.10^{ – 7}}{\left( {{{2.10}^3}} \right)^2}.\left( {{{5.10}^{ – 4}}} \right)\)
\(L = 2,{512.10^{ – 3}}\left( H \right)\)
Suất điện động tự cảm \({e_{tc}} = – L{{\Delta i} \over {\Delta t}}\) (dấu trừ thể hiện định luật Len-xơ)
a) Từ t1 = 0 đến t2= 0,05 (s):\(\Delta t = 0,05\left( s \right)\)
Ta có: \({e_{tc}} =2,{512.10^{ – 3}}.{{5 – 0} \over {0,05}} = 0,25\left( V \right)\)
b) Từ thời điểm t = 0,05 về sau: thì \(\Delta I = 0 \Rightarrow {e_{tc}} = 0\)

