Bài 1: Trong mặt phẳng (\( \alpha\)) cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn đường thẳng \(a,b,c,d\) song song với nhau và không nằm trên (\( \alpha\)). Trên \(a, b, c\) lần lượt lấy ba điểm \(A’, B’, C’\) tùy ý
a) Hãy xác định giao điểm \(D’\) của đường thẳng \(d\) với mặt phẳng \((A’B’C’)\)
b) Chứng minh \(A’B’C’D’\) là hình bình hành
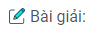
a) Gọi \(O = AC ∩ BD\); \(O’\) là trung điểm \(A’C’\) thì \(OO’ // AA’\)
\(\Rightarrow OO’// d // b\) mà \(O \in BD \subset mp (b;d)\) ( mặt phẳng xác định bởi hai đường thẳng song song); \(d ∩ B’O’ = D’\) là điểm cần tìm
b) \(mp(a;d) // mp( b;c)\) , mặt phẳng thứ 3 \((A’B’C’D’)\) cắt hai mặt phẳng trên theo hai giao tuyến song song : \(A’D’ // B’C’\). Chứng minh tương tự được \(A’B’ // D’C’\). Từ đó suy ra \(A’B’C’D’\) là hình bình hành.
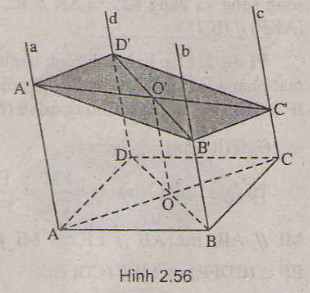
Bài 2: Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Gọi \(M\) và \(M’\) lần lượt là trung điểm của các cạnh \(BC\) và \(B’C’\)
a) Chứng minh rằng \(AM\) song song với \(A’M’\).
b) Tìm giao điểm của mặt phẳng \((AB’C’)\) với đường thẳng \(A’M\)
c) Tìm giao tuyến \(d\) của hai mặt phẳng \((AB’C’)\) và \((BA’C’)\)
d) Tìm giao điểm \(G\) của đường thẳng \(d\) với mặt phẳng \((AM’M)\)
Chứng minh \(G\) là trọng tâm của tam giác \(AB’C’\).
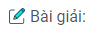
a) \(ABC.A’B’C’\) là hình lăng trụ tam giác nên ta có: \(AA’//MM’\) và \(AA’=MM’\) nên suy ra \(AA’M’M\) là hình bình hành.
Do đó: \(AM//A’M’\)
b) Trong \(mp (AA’M’M)\), gọi \(K=MA’ ∩ AM’ \),
Advertisements (Quảng cáo)
\(K =A’M\cap (AB’C’)\)
c) Trong \((ABB’A’)\) gọi \(O= AB’\cap A’B\)
Do đó: \((AB’C’)\cap (BA’C’)=d ≡ C’O\)
d) Trong \((AB’C’)\): gọi \(G= C’O ∩ AM’\),
\(G \in AM’\subset ( AMM’)\) nên \(G=d\cap (AMM’)\).
Mà \(O, M’\) lần lượt là trung điểm \(AB’\) và \(B’C’\) nên \(G\) là trọng tâm của tam giác \(AB’C’\).
Bài 3: Cho hình hộp \(ABCD.A’B’C’D’\)
a) Chứng minh rằng hai mặt phẳng \((BDA’)\) và \((B’D’C)\) song song với nhau
b) Chứng minh rằng đường chéo \(AC’\) đi qua trọng tâm \({G_{1},{G_{2}}}\) của hai tam giác \(BDA’\) và \(B’D’C\)
c) Chứng minh \({G_{1},{G_{2}}^{}}^{}\) chia đoạn \(AC’\) thành ba phần bằng nhau
Advertisements (Quảng cáo)
d) Gọi \(O\) và \(I\) lần lượt là tâm của các hình bình hành \(ABCD\) và \(AA’C’C\). Xác định thiết diện của mặt phẳng \((A’IO)\) với hình hộp đã cho
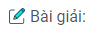
a) Tứ giác \(BDD’B’\) và \(A’BCD\) là hình bình hành nên: \(BD // B’D’\) \(\Rightarrow BD // (B’D’C)\)
và \(BA’ // CD’ \Rightarrow BA’ // ( B’D’C)\)
Từ đó suy ra \(( BDA’) //(B’D’C)\)
b) Gọi \(O,O’\) lần lượt là tâm của hình bình hành \(ABCD,A’B’C’D’\)
Gọi \({G_{1}}^{}\), \({G_{2}}^{}\) là giao điểm của \(AC’\) với \(A’O\) và \(CO’\)
\(\Delta {G_1}OA\) đồng dạng \(\Delta {G_1}A’C’\)
\( \Rightarrow {{{G_1}O} \over {{G_1}A’}} = {{OA} \over {A’C’}} = {1 \over 2} \Rightarrow {{A{G_1}} \over {A’O}} = {2 \over 3}\)
\(\Rightarrow G_1\) là trọng tâm \(\Delta A’BD\).
Chứng minh tương tự ta có: \(G_2\) là trọng tâm \(\Delta B’D’C\).
Vậy \(AC’\) đi qua \(G_1,G_2\).
c) Chứng minh
\( \frac{A{G_{1}}^{}}{{G_{1}C}^{}}\) = \( \frac{AO}{A’C’} = \frac{1}{2}\) (vì \(\Delta G_1OA\) đồng dạng \(\Delta G_1 A’C’\))
\( \frac{C'{G_{2}}^{}}{{G_{2}A}^{}}\) = \( \frac{C’O’}{CA} = \frac{1}{2}\) (vì \(\Delta G_2C’O’\) đồng dạng \(\Delta G_2 AC\))
Từ đó suy ra: \( {AG_{1} = {G_{1}{G_{2}= {G_{2}C’}^{}}^{}}^{}}^{}\)
d) \((A’IO) ≡ (AA’C’C)\) suy ra thiết diện là \(AA’C’C\)
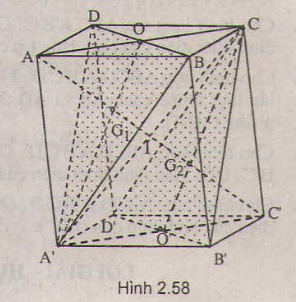
Bài 4: Cho hình chóp \(S.ABCD\). Gọi \(A_1\) là trung điểm của cạnh \(SA\) và \(A_2\) là trung điểm của đoạn \(AA_1\). Gọi \((α)\) và \((β)\) là hai mặt phẳng song song với mặt phẳng \((ABCD)\) và lần lượt đi qua \(A_1,A_2\). Mặt phẳng \((α)\) cắt các cạnh \(SB, SC, SD\) lần lượt tại \(B_1, C_1, D_1\). Mặt phẳng \((β)\) cắt các cạnh \(SB, SC, SD\) lần lượt tại \(B_2, C_2, D_2\). Chứng minh:
a) \(B_1, C_1, D_1\) lần lượt là trung điểm của các cạnh \(SB, SC, SD\)
b) \(B_1B_2 = B_2B\), \(C_1C_2 = C_2C\), \(D_1D_2 = D_2D\)
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác \(ABCD\).
a) \((α) // (ABCD) ⇒ A_1 B_1 // AB\) Mặt khác \(A_1\) là trung điểm của \(SA\) nên \(A_1B_1\) là đường trung bình của tam giác \(SAB\) \( ⇒B_1\) là trung điểm của \(SB\). Chứng minh tương tự với các điểm còn lại.
b) Ta có \(A_2B_2\) là đường trung bình hình thang \(ABB_1A_1\) nên \(B_1B_2=B_2B\). Chứng minh tương tự ta được: \(C_1C_2 = C_2C\), \(D_1D_2 = D_2D\).
c) Có hai hình chóp cụt: \(ABCD.{A_1}{B_1}{C_1}{D_1};ABCD.{A_2}{B_2}{C_2}{D_2}\).

