Bài 17: Trong mặt phẳng tọa đọ Oxy hãy tìm tọa độ các đỉnh M, N của hình vuông AMBN, biết tọa độ hai đỉnh A(1; 1) và B(3; 5).

Giả sử M(x; y) là đỉnh của hình vuông AMBN.
Ta có: \(\left\{ \matrix{
\left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {BM} } \right| \hfill \cr
\overrightarrow {AM} \bot \overrightarrow {BM} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
A{M^2} = B{M^2} \hfill \cr
\overrightarrow {AM} .\overrightarrow {BM} = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
{(x – 1)^2} + {(y – 1)^2} = {(x – 3)^2} + {(y – 5)^2} \hfill \cr
(x – 1)(x – 3) + (y – 1)(y – 5) = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
x + 2y = 8 \hfill \cr
{x^2} + {y^2} – 4x – 6y + 8 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 4 \hfill \cr
y = 2 \hfill \cr} \right.\)
hoặc
\(\left\{ \matrix{
x = 0 \hfill \cr
y = 4 \hfill \cr} \right.\)
Vậy M(4; 2), N(0; 4) hoặc M(0; 4), N(4; 2).
Bài 18: Biểu diễn hình học tập nghiệm của hệ bất phương trình
\(\left\{ \matrix{
2y – x \le 6 \hfill \cr
9x + 4y \le 56 \hfill \cr
3x + 5y \ge 4 \hfill \cr} \right.\)

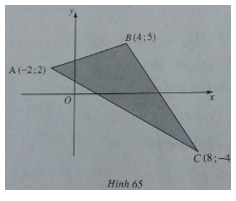
(h.65) Tập nghiệm là miền tam giác ABC (kể cả biên).
 Bài 19: Cho các số liệu thống kê ghi trong bảng sau
Bài 19: Cho các số liệu thống kê ghi trong bảng sau
Thời gian giải xong một bài tập Toán của 44 học sinh lớp 10A, trường Trung học phổ thông K
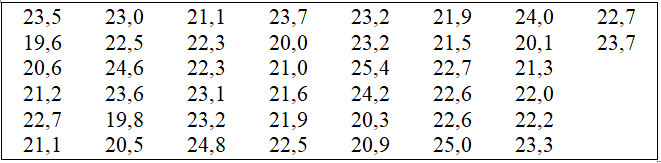
a) Lập bảng phân bố tần số và tần suất ghép lớp với các lớp như sau:
[19,5; 20,5); [20,5; 21,5); [21,5; 22,5); [22,5; 23,5); [23,5; 24,5); [24,5; 25,5].
Advertisements (Quảng cáo)
b) Dựa vào bảng phân bố tần suất ghép lớp đã lập hãy nêu nhận xét về thời gian làm một bài tập của 44 học sinh kể trên.
c) Hãy tính số trung bình cộng \(\overline x \), phương sai \(s_x^2\) và độ lệch chuẩn \({s_x}\) của các số liệu thống kê đã cho.
d) Giả sử rằng, cũng khảo sát thời gian giải xong một bài tập Toán của học sinh ở các lớp 10B, 10C của trường K, rồi tính các số trung bình cộng, phương sai và độ lệch chuẩn của các số liệu thống kê ở từng lớp, ta thu được kết quả sau:
Ở lớp 10B có \(\overline y = 20\) phút, \(s_y^2 = 1,{s_y} = 1\) phút
Ở lớp 10C có \(\overline z = 22,4\) phút, \(s_z^2 = 1,{s_z} = 1\) phút
Hãy so sánh thời gian giải xong một bài tập Toán của học sinh ở ba lớp 10A, 10B, 10C đã cho.
e) Vẽ biểu đồ tần suất hình cột mô tả bảng phân bố tần suất ghép lớp đã lập được.

a) Thời gian giải xong một bài tập toán của 44 học sinh lớp 10A, trường Trung học phổ thông K
|
Lớp thời gian (phút) |
Tần số |
Tần suất (%) |
|
[19,5;20,5) [20,5; 21,5) [21,5; 22,5) [22,5; 23,5) [23,5; 24,5) [24,5; 25,5] |
5 7 10 12 6 4 |
11,36 15,91 22,73 27,27 13,64 9,09 |
|
Cộng |
44 |
100 (%) |
b) Nhận xét:
Trong 44 học sinh đã được khảo sát ta thấy:
Chiểm tỉ lệ thấp nhất (9,09%) là những học sinh có thời gian giải xong một bài tập toán từ 24,5 phút đến 25,5 phút.
Advertisements (Quảng cáo)
Chiểm tỉ lệ cao nhất (27,27%) là những học sinh có thời gian giải xong một bài tập toán từ 22,5 phút đến dưới 23,5 phút.
Đa số (79,55%) là những học sinh có thời gian giải xong bài tập toán đó từ 20,5 phút đến dưới 24,5 phút.
c) Sử dụng bảng phân bố tần số ghép lớp đã lập, ta tính được \(\overline x = 22,4\) phút, \(s_x^2 = 2,1,{s_x} = 1,4\) phút
d) Ta có \(\overline x \approx \overline z = 22,4\) phút >20 phút = \(\overline y \) và \(s_x^2 = 2,1 > 1 = s_z^2\) nên thời gian giải xong bài tập toán đó của các học sinh lớp 10C là đồng đều hơn các học sinh lớp 10A.
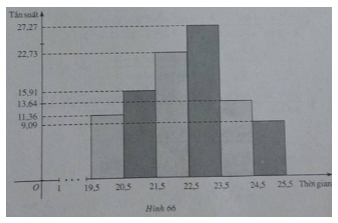
e) Biểu đồ tần suất hình cột về thời gian (phút) giải xong một bài tập toán của 44 học sinh lớp 10A, trường Trung học phổ thông K (h.66)
Bài 20: Chứng minh rằng
a) \({{\sqrt {1 + \cos \alpha } + \sqrt {1 – \cos \alpha } } \over {\sqrt {1 + \cos \alpha } – \sqrt {1 – \cos \alpha } }} = \cot ({\alpha \over 2} + {\pi \over 4})\) \((\pi < \alpha < 2\pi )\)
b) \({{\cos 4a\tan 2a – \sin 4a} \over {\cos 4a\cot 2a + \sin 4a}} = – {\tan ^2}2a\)
c) \({{{{\sin }^2}2a + 4{{\sin }^2}a – 4} \over {1 – 8{{\sin }^2}a – \cos 4a}} = {1 \over 2}{\cot ^4}a\)
d) \(1 + 2\cos 7a = {{\sin 10,5a} \over {\sin 3,5a}}\)
e) \({{\tan 3a} \over {\tan a}} = {{3 – {{\tan }^2}a} \over {1 – 3{{\tan }^2}a}}\)

a) Vì \(\sqrt {1 + \cos \alpha } = – \sqrt 2 \cos {\alpha \over 2}(do{\pi \over 2} < {\alpha \over 2} < \pi )\)
\(\sqrt {1 – \cos \alpha } = \sqrt 2 \sin {\alpha \over 2}\) cho nên
\({{\sqrt {1 + \cos \alpha } + \sqrt {1 – \cos \alpha } } \over {\sqrt {1 + \cos \alpha } – \sqrt {1 – \cos \alpha } }} = {{ – \sqrt 2 \cos {\alpha \over 2} + \sqrt 2 \cos {\alpha \over 2}} \over { – \sqrt 2 \cos {\alpha \over 2} – \sqrt 2 \cos {\alpha \over 2}}}\)
\( = {{\cos {\alpha \over 2} – \sin {\alpha \over 2}} \over {\cos {\alpha \over 2} + \sin {\alpha \over 2}}} = {{1 – \tan {\alpha \over 2}} \over {1 + \tan {\alpha \over 2}}} = \tan ({\pi \over 4} – {\alpha \over 2})\)
\( = \cot ({\alpha \over 2} + {\pi \over 4})\)
b) \(\eqalign{
& = {{\cos 4a\tan 2a – \sin 4a} \over {\cos 4a\cot 2a + \sin 4a}} \cr
& = {{\cos 4a\sin 2a – \sin 4a\cos 2a} \over {\cos 4a\cos 2a + \sin 4a\sin 2a}}.\tan 2a \cr} \)
\( = {{ – \sin 2a} \over {\cos 2a}}\tan 2a = – {\tan ^2}2a$\)
c) \(\eqalign{
& {{{{\sin }^2}2a + 4{{\sin }^2}4a} \over {1 – {{\sin }^2}a – \cos 4a}} \cr
& = {{4{{\sin }^2}a{{\cos }^2}a + 4({{\sin }^2}a – 1)} \over {1 – 8{{\sin }^2}a – (1 – 2{{\sin }^2}2a)}} \cr} \)
\({{4{{\cos }^2}a({{\sin }^2}a – 1)} \over {8{{\sin }^2}a(co{s^2}a – 1)}} = {1 \over 2}{\cot ^4}a.\)
d) \(\eqalign{
& {{\sin 10,5a} \over {\sin 3,5a}} = {{\sin (7 + 3,5a)} \over {\sin 3,5a}} \cr
& = {{\sin 7a\cos 3,5a + \cos 7a\sin 3,5a} \over {\sin 3,5a}} \cr} \)
\( = {{\sin 3,5a(2{{\cos }^2}3,5a + \cos 7a)} \over {\sin 3,5a}}\)
\( = (2{\cos ^2}3,5a – 1) + 1 + cos7a\)
\( = 2cos7a + 1.\)
e) \(\eqalign{
& {{\tan (a + 2a)} \over {\tan a}} = {{\tan a + \tan 2a} \over {\tan a(1 – {\mathop{\rm tanatan}\nolimits} 2a}} \cr
& = {{\tan a + {{2\tan a} \over {1 – {{\tan }^2}a}}} \over {\tan a(1 – {{2{{\tan }^2}a} \over {1 – {{\tan }^2}a}})}} \cr} \)
\( = {{3 – {{\tan }^2}a} \over {1 – 3{{\tan }^2}a}}$\).

