Bài 8: Cho ngũ giác đều A0A1A2A3A4 nội tiếp đường tròn tâm O (các đỉnh được sắp xếp theo chiều ngược chiều quay của kim đồng hồ). Tính số đo (độ và radian) \(\overparen{{A_0}{A_i}}\), \(\overparen{{A_i}{A_j}}\)
Đáp án
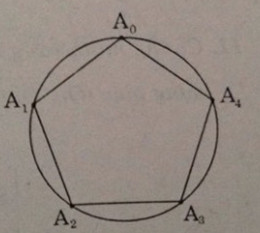
Ta có:
\(sd \overparen{{A_0}{A_i}}= i{{2\pi } \over 5} + k2\pi \)
Hay i.720 + k3600
Với mọi i = 0, 1, 2, 3, 4 k ∈ Z
Từ đó, theo hệ thức Sa-lơ:
\(\eqalign{
& sd \overparen{{A_i}{A_j}}= sd\overparen{{A_0}{A_j}} – sd\overparen{{A_0}{A_i}} + k2\pi \cr
& = (j – i){{2\pi } \over 5} + k2\pi \cr} \)
Hay (j – i).720 + 3600 (i, j = 0, 1, 2, 3, 4 ; i ≠ j; k ∈ Z)
Advertisements (Quảng cáo)
Bài 9: Tìm góc lượng giác (Ou, Ov) có số đo dương lớn nhất, biết một góc lượng giác (Ou, Ov) có số đo:
a) -900
b) 10000
c) \({{30\pi } \over 7}\)
d) \( – {{15\pi } \over {11}}\)
Advertisements (Quảng cáo)
Đáp án
+ Nếu góc lượng giác có số đo là \(a^0\) thì ta cần xác định số nguyên k để : 0o < ao + k360o ≤ 3600
Khi đó: ao + k360o là số dương nhỏ nhất cần tìm.
a) Với a = -900 thì k = 1. Số dương nhỏ nhất cần tìm là 270
b) Với a = 1000o thì k = -2. Số dương nhỏ nhất cần tìm là 280
c) Với α = \({{30\pi } \over 7}\) thì k = -2. Số dương nhỏ nhất cần tìm là: \({{2\pi } \over 7}\)
d) Với α = \( – {{15\pi } \over {11}}\) thì k = 1. Số dương nhỏ nhất cần tìm là: \({{7\pi } \over {11}}\)
Bài 10: Tìm số đo radian α ,-π < α ≤π, của góc lượng giác có cùng tia đầu, tia cuối với góc trên mỗi hình sau.
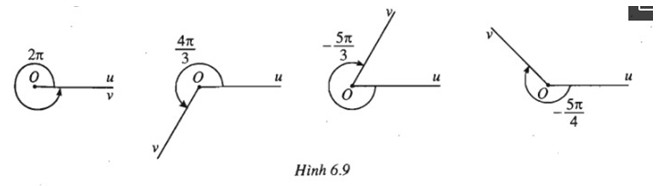
Đáp án
a) α = 0
b) \(\alpha = – {{2\pi } \over 3}( = {{4\pi } \over 3} – 2\pi )\)
c) \(\alpha = {\pi \over 3}\)
d) \(\alpha = {{3\pi } \over 4}( = 2\pi – {{5\pi } \over 4})\)

