Câu C1: Khi ta bước từ một thuyền nhỏ lên bờ thì thuyền lùi lại. Hãy giải thích.
Lực đẩy Ac-si-mét cân bằng với trọng lực của “người + thuyền” nên hệ là hệ kín có tổng động lượng trước khi người bước lên bằng \(\overrightarrow 0 \). Áp dụng định luật bảo toàn động lượng, ta có:
\(M\overrightarrow V + m\overrightarrow v = \overrightarrow 0 \) hay \(\overrightarrow V = – {m \over M}\overrightarrow v \Leftrightarrow \)Thuyền lùi lại.
Câu C2: Tại sao máy bay cánh quạt lại không thể coi là máy bay phản lực?
Máy bay cánh quạt không thể coi là máy bay phản lực vì nó chuyển động nhờ phản lực của không khí tác dụng vào cánh quạt chứ không phải bằng cách phụt hỗn hợp khí cháy về phía sau.
Bài 1: Hai xe lăn nhỏ có khối lượng m1=300g và m2 = 2kg chuyển động trên mặt phẳng ngang ngược chiều nhau với các vận tốc tương ứng v1=2m/s và v2=0,8m/s. Sau khi va chạm, hai xe dính vào nhau và chuyển động với cùng vận tốc. Tìm độ lớn và chiều của vận tốc này. Bỏ qua mọi lực cản.
Mặt phẳng ngang, không ma sát nên hệ hai xe lăn là kín. Áp dụng định luật bảo toàn động lượng:
\(({m_1} + {m_2})\overrightarrow v = {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} \)
\(\Rightarrow \overrightarrow v = {{{m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} } \over {{m_1} + {m_2}}}(1)\)
Advertisements (Quảng cáo)
Chọn chiều dương là chiều chuyển động ban đầu của xe 1 thì (1)
\( \Rightarrow v = {{{m_1}{v_1} – {m_2}{v_2}} \over {{m_1} + {m_2}}} = {{0,3.2 – 2.0,8} \over {0,3 + 2}} \approx – 0,43(m/s)\)
Sau va chạm 2 xe chuyển động cùng chiều xe 2 (trước va chạm) với tốc độ 0,43(m/s).
Bài 2: Một tên lửa có khối lượng tổng cộng M = 10 t đang bay với vận tốc V=200m/s đối với Trái Đất thì phụt ra phía sau (tức thời) khối lượng khí m=2t với vận tốc v=500m/s đối với tên lửa . Tìm vận tốc tức thời của tên lửa sau khi phụt khí với giả thiết toàn bộ khối lượng khí được phụt ra cùng một lúc.
Vận tốc của khí đối với Trái Đất: \(\overrightarrow v = \overrightarrow {{v_0}} + \overrightarrow V \)
\(\overrightarrow {{v_0}} \) là vận tốc của khí đối với đất: v0=500m/s.
Advertisements (Quảng cáo)
\(\overrightarrow V \) là vận tốc của tên lửa đối với đất trước khi phụt khí.
Gọi \(\overrightarrow {V’} \) là vận tốc của tên lửa đối với đất sau khi phụt khí.
Coi hệ “ tên lửa” là kín trong thời gian phụt khí, áp dụng định luật bảo toàn động lượng:
\(\eqalign{ & M\overrightarrow V = (M – m)\overrightarrow {V’} + m\overrightarrow v \cr&\;\;\;\;\;\;\;\;\,= (M – m)\overrightarrow {V’} + m(\overrightarrow {{v_0}} + \overrightarrow V ) \cr & \overrightarrow {V’} = {{(M – m)\overrightarrow V – m\overrightarrow {{v_0}} } \over {M – m}} = \overrightarrow V – {m \over {M – m}}\overrightarrow {{v_0}} (1) \cr} \)
Chọn chiều dương là chiều chuyển động ban đầu của tên lửa thì (1)
\(\eqalign{ & \Rightarrow V’ = V – {m \over {M – m}}( – {v_0}) = V + {m \over {M – m}}{v_0} \cr & V’ = 200 + {2 \over {10 – 2}}.500 = 325(m/s). \cr} \)
Tên lửa chuyển động theo hướng cũ với vận tốc 325m/s.
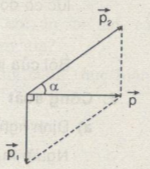
Bài 3: Một viên đạn có khối lượng m=2kg khi bay đến điểm cao nhất của quỹ đạo parabol với vận tốc v=200m/s theo phương nằm ngang thì nổ thành hai mảnh. Một mảnh có khối lượng m1=1,5kg văng thẳng đứng xuống dưới với vận tốc v1 cũng bằng 200m/s. Hỏi mảnh kia bay theo hướng nào và với vận tốc bằng bao nhiêu?
p = mv = 2.200 = 400(kgm/s).
p1 = m1v1 = 1,5.200 = 300(kgm/s);
m2 = m – m1 = 0,5(kg)
Coi hệ “đạn nổ” là hệ kín trong thời gian nổ, áp dụng định luật bảo toàn động lượng :
\(\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Từ hình vẽ, ta có:
\(\eqalign{ & {p_2} = \sqrt {p_1^2 + {p^2}} = \sqrt {{{300}^2} + {{400}^2}} = 500(kgm/s) \cr & {v_2} = {{{p_2}} \over {{m_2}}} = {{500} \over {0,5}} = 1000(kgm/s) \cr & \tan \alpha = {{{p_1}} \over p} = {3 \over 4} \Rightarrow \alpha = {37^0}. \cr} \)
Mảnh hai bay lên theo hướng hợp với hướng chuyển động ban đầu góc \(\alpha = {37^0}\) với tốc độ 1000m/s.