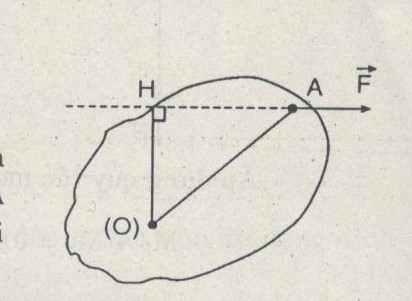
Câu C1: Khoảng cách từ trục quay tới giá của lực và khoảng cách từ điểm đặt của lực tới trục quay có phải là một không ?
Giải
Khoảng cách từ trục quay tới giá của lực OH và khoảng cách từ điểm đặt A của lực tới trục quay OA là hai đại lượng khác nhau.
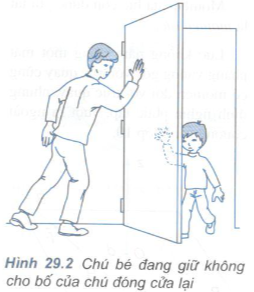
Câu C2: Dựa vào quy tắc momen, hãy lí giải hiện tượng hai người đẩy cửa ở Hình 29.2.
Giải
Bố tác dụng lực F1 lớn nhưng tay đòn d1 của \(\overrightarrow {{F_1}} \) nhỏ
Con tác dụng lực F2 nhỏ nhưng tay đòn d1 của \(\overrightarrow {{F_2}} \) lớn.
\(=>\) M1 + M2 = 0 \(=>\) Cánh cửa đứng yên.
Bài 1: Ở trường hợp nào sau đây, lực tác dụng làm cho vật rắn quay quanh trục ?
A. Lực có giá nằm trong mặt phẳng vuông góc với trục quay và cắt trục quay.
B. Lực có giá song song với trục quay.
C. Lực có giá cắt trục quay.
D. Lực có giá nằm trong mặt phẳng vuông góc với trục quay và không cắt trục quay.
Advertisements (Quảng cáo)
Giải
Chọn D.
Bài 2: Một thanh chắn đường dài 7,8 m, có trọng lượng 210 N và có trọng tâm cách đầu bên trái 1,2 m (Hình 29.7). Thanh có thể quay quanh một trục nằm ngang ở cách đầu bên trái 1,5 m. Hỏi phải tác dụng vào đầu bên phải một lực bằng bao nhiêu để giữ thanh ấy nằm ngang?

Giải
Thanh chắn là vật rắn có trục quay cố định (O) cân bằng dưới tác dụng của 2 lực gây momen \(\overrightarrow P \) và \(\overrightarrow F \).

Áp dụng quy tắc momen, ta có :
Advertisements (Quảng cáo)
\(\eqalign{ & {M_P} + {M_F} = 0 < = > P.OG – F.OB = 0\cr& < = > F = {{OG} \over {OB}}.P \cr & Với\,\left\{ \matrix{ OG = OA – GA = 1,5 – 1,2 = 0,3(m) \hfill \cr OB = AB – OA = 7,8 – 1,5 = 6,3(m) \hfill \cr P = 210N \hfill \cr} \right. \cr} \)
tính được \(F = {{0,3} \over {6,3}}.210 = 10(N)\)
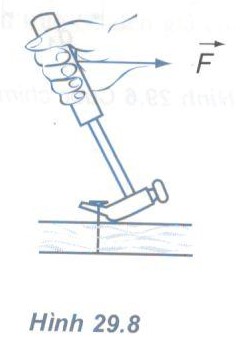
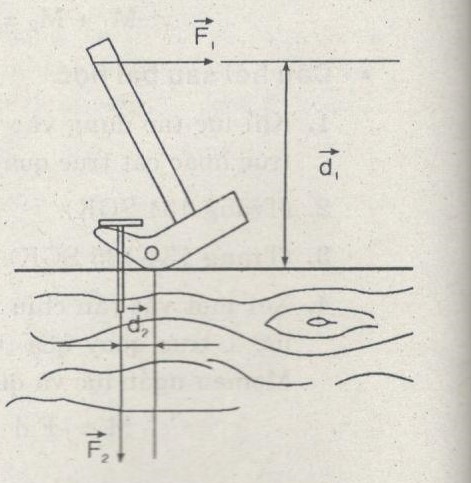
Bài 3: Một chiếc búa đinh dùng để nhổ một chiếc đinh (Hình 29.8). Hãy vẽ trục quay của búa, các lực của tay và của đinh tác dụng vào búa và các tay đòn của hai lực đó.
Giải
Khi búa đang ở tư thế nhổ đinh như hình vẽ thì nó là vật có trục quay tạm thời đi qua điểm tiếp xúc (O) giữa búa và mặt tấm gỗ.
Tay đòn của lực \(\overrightarrow {{F_1}} \) do tay tác dụng lên búa là d1.
Tay đòn của lực \(\overrightarrow {{F_2}} \) do đinh tác dụng lên búa là d2.
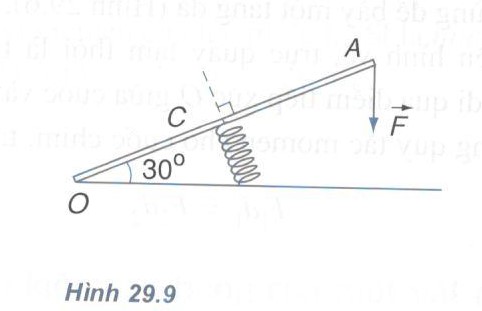
Bài 4: Thanh OA có khối lượng không đáng kể, có chiều dài 20 cm, quay dễ dàng quanh trục nằm ngang O. Một lò xo gắn vào điểm giữa C. Người ta tác dụng vào đầu A của thanh một lực F =20 N hướng thẳng xuống dưới (Hình 29.9). Khi thanh ở trạng thái cân bằng, lò xo có phương vuông góc với OA, và OA làm thành một góc α = 300 so với đường thẳng nằm ngang.
a) Tính phản lực N của lò xo vào thanh.
b) Tính độ cứng k của lò xo, biết lò xo ngắn đi 8 cm so với lúc không bị nén.
Giải
a)
\(\eqalign{ & {m_{OA}} \approx 0 \cr & OA = 20cm \cr & F = 20N \cr & CO = {{OA} \over 2} = 10\,cm \cr & \alpha = {30^0} \cr & = > OH = OA.cos{30^0} = 10\sqrt 3 \,cm \cr} \)
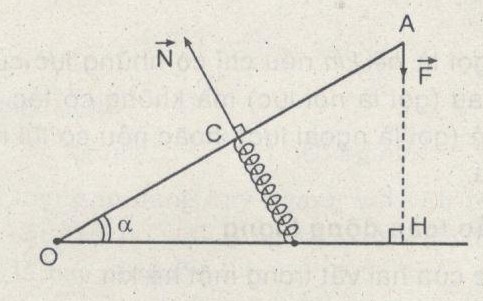
Thanh OA là vật rắn có trục quay (O) cân bằng dưới tác dụng của hai lực có momen lực \(\overrightarrow F \) có tay đòn OH; lực đàn hồi \(\overrightarrow N \) có tay đòn OC.
Áp dụng quy tắc momen ta có :
\(\eqalign{ & N.OC = F.OH \cr & = > N = {{OH} \over {OC}}.F = 20\sqrt 3 (N) \cr} \)
b) \(\overrightarrow N \) là lực đàn hồi của lò xo tác dụng lên thanh nên áp dụng định luật Húc, ta có :
\(\eqalign{ & N = k.\Delta l \cr & = > \,k = {N \over {\Delta l}} = {{20\sqrt 3 } \over {0,08}} \approx 433(N/m) \cr} \)

