Câu C1: Hãy viết công thức của định luật II Niu-tơn cho mỗi vật.
Giải :
Công thức định luật II khi chọn trục x’x theo chiều lực \(\overrightarrow F \)
\(\left\{ \matrix{ cho\,vật\,{m_1}:\,{m_1}a = F – T – {F_{ms1}} \hfill \cr cho\,vật\,{m_2}\,:\,{m_2}a = {T’} – {F_{ms2}} \hfill \cr} \right.\)
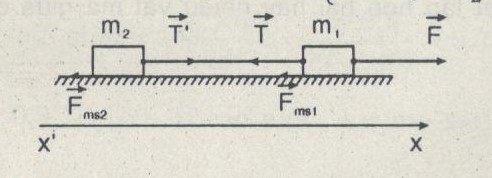
Câu C2: Các vật trong hệ ở Hình 24.3 có thể đứng yên hoặc chuyển động theo những khả năng nào ? Làm thế nào để biết được khả năng xảy ra ?
Giải
So sánh P1 và P2x ta biết được xu hướng chuyển động của hệ.
Trong bài : P1 > P2x nên nếu chuyển động được thì hệ chuyển động sao cho m1 xuống
\(=>\) Chiều lực ma sát cùng chiều \(\overrightarrow {{P_{2x}}} \). Muốn biết có chuyển động được không, ta so sánh P1 và P2x + FM.
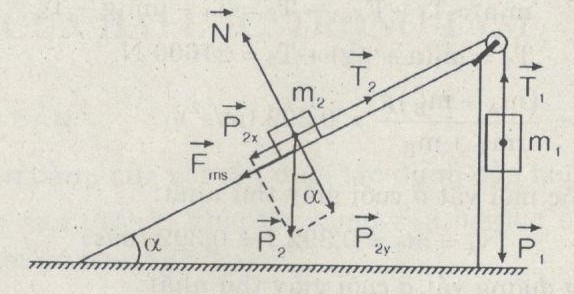
Nếu P1 > P2x + FM thì hệ chuyển động được từ trạng thái nghỉ.
Nếu P1 < P2x + FM thì hệ đứng yên.
( Bài toán không cho biết \({\mu _{n\,}}\) để tính FM, lời giải dựa vào quan hệ P1 > P2x + Fmst để khẳng định m1 đi xuống là sai).
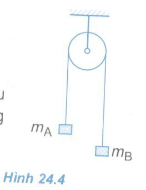
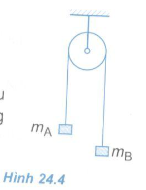
Bài 1: Cho hệ vật như ở Hình 24.4. Biết \({m_A} > {m_B}\). Gia tốc của hai vật là a. Lực căng dây bằng bao nhiêu ?
A. \({m_A}g\) B. \(({m_A} + {m_B})g\)
C. \(({m_A} – {m_B})g\) D. \({m_A}\left( {g – a} \right)\)
Advertisements (Quảng cáo)
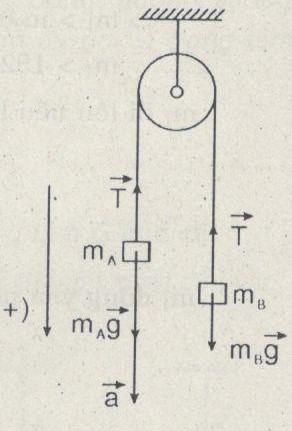
Giải :
Chọn D. (Áp dụng định luật II cho vật mA:
\(\eqalign{ & {m_A}\overrightarrow a = {m_A}\overrightarrow g + \overrightarrow T \cr & = > {m_A}a = {m_A}g – T = > T = {m_A}\left( {g – a} \right) \cr} \)
Bài 2: Một đầu tàu có khối lượng 50 tấn được nối với hai toa, mỗi toa có khối lượng 20 tấn. Đoàn tàu bắt đầu chuyển động với gia tốc a = 0,2 m/s2. Hệ số ma sát lăn giữa bánh xe với đường ray là 0,05. Hãy tính:
a) Lực phát động tác dụng lên đoàn tàu.
b) Lực căng ở những chỗ nối toa.
Giải :
a) Đường ngang nên
Advertisements (Quảng cáo)
\({F_{ms}} = \mu mg;\,{F_{ms1}} = \mu {m_1}g\,;\,{F_{ms2}} = \mu {m_2}g\).
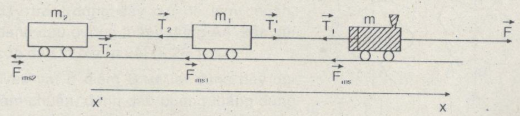
Áp dụng định luật II cho hệ vật :
\(\eqalign{ & a = {{F – {F_{ms}} – {F_{ms1}} – {F_{ms2}}} \over {m + {m_1} + {m_2}}} \cr & = {{F – \mu g(m + {m_1} + {m_2})} \over {m + {m_1} + {m_2}}} \cr & F = (m + {m_1} + {m_2})(a + \mu g) = 62100\,N \cr} \)
b) Áp dụng định luật II cho toa 2 :
\(\eqalign{ & {m_2}a = {T_2} – {F_{ms2}} = {T_2} – \mu {m_2}g \cr & {T_2} = {m_2}(a + \mu g) = 13800\,(N). \cr} \)
Áp dụng định luật cho toa 1 :
\(\eqalign{ & {m_1}a = {T_1} – {F_{ms1}} – {T_2} = {T_1} – \mu {m_1}g – {T_2} \cr & {T_1} = {m_1}(a + \mu g) + {T_2} = 27600\,N \cr} \).
Bài 4: Trong ví dụ ở mục 2 của bài, nếu cho m1 những giá trị khác nhau (các dữ kiện khác giữ nguyên) thì hiện tượng có thể diễn ra những khả năng nào ? Tìm phạm vi giá trị của m1 để xảy ra mỗi khả năng ấy.
Giải :
Với giả thiết \({\mu _n} = {\mu _t} = 0,3\) thì m1 sẽ đi xuống nếu \({P_1} > {P_{2x}} + {F_M}\)
\(\eqalign{ & < = > {m_1}g > {m_2}g\sin \alpha + {\mu _n}{m_2}g\cos \alpha \cr & < = > {m_1} > {m_2}(\sin \alpha + {\mu _n}{\rm{cos}}\alpha {\rm{)}} \cr & {{\rm{m}}_1} > 152\,g \cr} \)
m1 đi lên nếu
\(\eqalign{ & {P_{2x}} > {P_1} + {F_M} < = > {P_1} < {P_{2x}} – {F_M} \cr & < = > {m_1}g < {m_2}g\sin \alpha – {\mu _n}{m_2}g\cos \alpha \cr & < = > {m_1} < {m_2}(\sin \alpha – {\mu _n}{\rm{cos}}\alpha {\rm{)}} \cr & {\rm{ < = > }}{{\rm{m}}_1} < 48\,g \cr} \).
m1 đứng yên nếu \(48 \le m \le 152(g)\).
Bài 3: Người ta vắt qua một chiếc ròng rọc nhẹ một đoạn dây, ở hai đầu có treo hai vật A và B có khối lượng là mA = 260 g và mB = 240 g (Hình 24.4). Thả cho hệ bắt đầu chuyển động.
a) Tính vận tốc của từng vật ở cuối giây thứ nhất.
b) Tính quãng đường mà từng vật đi được trong giây thứ nhất.
Bỏ qua ma sát ở ròng rọc, coi dây là không dãn.
Giải :
\({v_0} = 0;a = {{({m_A} – {m_B})g} \over {{m_A} + {m_B}}} = 0,392(m/{s^2})\)
a) Vận tốc mỗi vật ở cuối giây thứ nhất:
\({v_1} = a{t_1} = 0,392.1 = 0,392(m/s)\)
b) Quãng đường vật ở cuối giây thứ nhất:
\({S_1} = {{at_1^2} \over 2} = 0,196(m)\)

