Câu 107: Tìm các tam giác cân trên hình dưới.
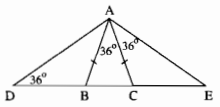
Ta có: AB = AC (gt) nên ∆ABC cân tại A.
\(\Rightarrow \widehat {ABC} = \widehat {ACB} = {{180^\circ – \widehat {BAC}} \over 2} = {{180^\circ – 36^\circ } \over 2} = 72^\circ \)
\(\widehat {BA{\rm{E}}} = \widehat {BAC} + \widehat {CA{\rm{E}}} = 36^\circ + 36^\circ = 72^\circ \)
\(\Rightarrow \widehat {BA{\rm{E}}} = \widehat {ABE}\) => ∆ABE cân tại E
\(\widehat E = 180^\circ – 2\widehat {ABE} = 180^\circ – 2.72^\circ = 36^\circ \)
\(\widehat {CA{\rm{E}}} = \widehat E\) nên ∆ACE cân tại C.
Trong ∆DAC, ta có:
\(\widehat {DAC} = 180^\circ – \left( {\widehat D + \widehat {AC{\rm{D}}}} \right) = 180^\circ – \left( {36^\circ + 72^\circ } \right) = 72^\circ \)
Vì \(\widehat {DAC} = \widehat {AC{\rm{D}}}\) nên ∆DAC cân tại D
\(\eqalign{
& \widehat {DAC} = \widehat {DAB} + \widehat {BAC} \cr
& \Rightarrow \widehat {DAB} = \widehat {DAC} – \widehat {BAC} = 72^\circ – 36^\circ = 36^\circ \cr} \)
\( \Rightarrow \widehat {DAB} = \widehat D\) nên ∆ABD cân tại B
\(\widehat {A{\rm{D}}E} = \widehat {A{\rm{ED}}} = 36^\circ \) nên ∆ADE cân tại A
Vậy có 6 tam giác cân trong hình trên.
Câu 108: Bạn Mai vẽ tia phân giác của một góc như sau: Đánh dấu trên hai cạnh của bốn góc bốn đoạn thẳng bằng nhau: OA = AB = OC = CD (hình dưới). Kẻ các đoạn thẳng AD, BC, chúng cắt nhau ở K. Hãy giải thích vì sao OK là tia phân giác của góc O.
 Chứng minh rằng:
Chứng minh rằng:
a) ∆OAD = ∆OCB
b) ∆KAB = ∆KCD
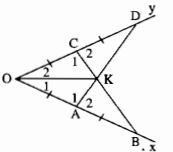
a) Xét ∆OAD và ∆OCB, ta có:
OA = OC (gt)
\(\widehat O\) chung
Advertisements (Quảng cáo)
OD = OB (gt)
Suy ra: ∆OAD = ∆OCB (c.g.c)
b) Ta có: ∆OAD = ∆OCB
Suy ra: \(\widehat D = \widehat B\) (hai góc tương ứng)
\(\widehat {{C_1}} = \widehat {{A_1}}\) (hai góc tương ứng)
Lại có: \(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (kề bù)
\(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (kề bù)
Suy ra: \(\widehat {{C_2}} = \widehat {{A_2}}\)
Xét ∆KCD và ∆KAB, ta có:
\(\widehat D = \widehat B\) (chứng minh trên)
CD = AB (gt)
\(\widehat {{C_2}} = \widehat {{A_2}}\) (chứng minh trên)
Suy ra: ∆KCD = ∆KAB (g.c.g) => KC = KA (hai cạnh tương ứng)
Xét ∆OCK = ∆OAK, ta có:
OC = OA (gt)
OK cạnh chung
Advertisements (Quảng cáo)
KC = KA (chứng minh trên)
Suy ra: ∆OCK = ∆OAK (c.c.c) => \(\widehat {{O_1}} = \widehat {{O_2}}\) (hai góc tương ứng)
Vậy OK là tia phân giác của góc O
Câu 109: Cho tam giác ABC cân tại A, kẻ \(BH \bot AC\). Gọi D là một điểm thuộc cạnh đáy BC. Kẻ \({\rm{D}}E \bot AC,DF \bot AB\). Chứng minh rằng DE + DF = BH.
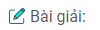
Kẻ \({\rm{DK}} \bot {\rm{BH}}\)
Ta có: \(BH \bot AC\left( {gt} \right)\)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau)
\( \Rightarrow \widehat {K{\rm{D}}B} = \widehat C\) (hai góc đồng vị)
Vì ∆ABC cân tại A nên \(\widehat B = \widehat C\) (tính chất tam giác cân)
Suy ra: \(\widehat {K{\rm{D}}B} = \widehat B\)
Xét hai tam giác vuông BFD và DKB, ta có:
\(\widehat {BF{\rm{D}}} = \widehat {DKB} = 90^\circ \)
BD cạnh huyền chung
\(\widehat {FB{\rm{D}}} = \widehat {K{\rm{D}}B}\) (chứng minh trên)
Suy ra: ∆BFD = ∆DKB (cạnh huyền, góc nhọn)
\( \Rightarrow \) DF = BK (hai cạnh tương ứng) (1)
Nối DH. Xét ∆DEH = ∆DKH, ta có:
\(\widehat {DEH} = \widehat {DKH} = 90^\circ \)
DH cạnh huyền chung
\(\widehat {EH{\rm{D}}} = \widehat {K{\rm{D}}H}\) (hai góc so le trong)
Suy ra: ∆DEH = ∆DKH (cạnh huyền, góc nhọn)
Suy ra: DE = HK (hai cạnh tương ứng) (2)
Mặt khác: BH = BK + HK (3)
Từ (1), (2) và (3) suy ra: DF + DE = BH
Câu 110: Cho tam giác ABC vuông tại A có \({{AB} \over {AC}} = {3 \over 4}\) và BC=15cm. Tính các độ dài AB, AC.
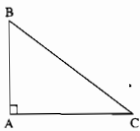
Theo đề bài, ta có:
\({{AB} \over {AC}} = {3 \over 4} \Rightarrow {{AB} \over 3} = {{AC} \over 4} \Rightarrow {{A{B^2}} \over 9} = {{A{C^2}} \over {16}}\)
Theo tính chất dãy tỉ số bằng nhau ta có:
\({{A{B^2}} \over 9} = {{A{C^2}} \over {16}} = {{A{B^2} + A{C^2}} \over {9 + 16}}\left( 1 \right)\)
Tam giác ABC vuông tại A
Áp dụng Pytago vào tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2}\left( 2 \right)\)
Từ (1) và (2) suy ra: \({{A{B^2}} \over 9} = {{A{C^2}} \over {16}} = {{B{C^2}} \over {25}} = {{{{15}^2}} \over {25}} = {{225} \over {25}} = 9\)
\({\rm{A}}{B^2} = 9.9 = 81 \Rightarrow AB = 9\left( {cm} \right)\) (vì AB > 0)
\(A{C^2} = 16.9 = 144 \Rightarrow AC = 12\left( {cm} \right)\) (vì AC > 0)

