Bài 8 Các trường hợp bằng nhau của tam giác vuông Sách Bài Tập Toán lớp 7 tập 1. Giải bài 99, 100, 101 trang 151 Sách Bài Tập Toán lớp 7 tập 1. Câu 99: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. …
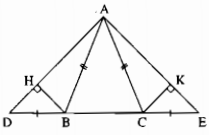
Câu 99: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD, kẻ CK vuông góc với AE. Chứng minh rằng:
a) BH = CK
b) ∆ABH = ∆ACK
a) Vì ∆ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Ta có: \(\widehat {ABC} + \widehat {AB{\rm{D}}} = 180^\circ \) (hai góc kề bù)
\(\widehat {ACB} + \widehat {AC{\rm{E}}} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\)
Xét ∆ABD và ∆ACE, ta có:
AB = AC (gt)
\(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\) (chứng minh trên)
BD = CE (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
\( \Rightarrow \widehat D = \widehat E\) (hai góc tương ứng)
Xét hai tam giác vuông BHD và CKE, ta có:
\(\widehat {BH{\rm{D}}} = \widehat {CKE} = 90^\circ \)
BD = CE (gt)
\(\widehat D = \widehat E\) (chứng minh trên)
Suy ra: ∆BHD = ∆CKE (cạnh huyền, góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Xét tam giác vuông AHB và ACK, ta có:
Advertisements (Quảng cáo)
\(\widehat {AHB} = \widehat {AKC} = 90^\circ \)
AB = AC (gt)
BH = CK (chứng minh trên)
Suy ra: ∆ABH = ∆ACK (cạnh huyền, cạnh góc vuông)
Câu 100: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Chứng minh rằng AI là tia phân giác của góc A.
 Từ I kẻ các đường thẳng vuông góc với các cạnh của tam giác ABC.
Từ I kẻ các đường thẳng vuông góc với các cạnh của tam giác ABC.
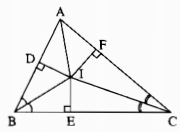
Kẻ: \(I{\rm{D}} \bot AB,IE \bot BC,{\rm{IF}} \bot {\rm{A}}C\)
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
\( \Rightarrow \) ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Advertisements (Quảng cáo)
Suy ra: ID = IE (hai cạnh tương ứng)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat {I{\rm{D}}A} = \widehat {IFA} = 90^\circ \)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: \(\widehat {DAI} = \widehat {FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat A\)
Câu 101: Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.
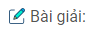
Xét ∆BMI và ∆CMI, ta có:
BM = CM (gt)
\(\widehat {BMI} = \widehat {CMI} = 90^\circ \)
MI cạnh chung
Suy ra: ∆BMI = ∆CMI (c.g.c)
\( \Rightarrow \) IB = IC (hai cạnh tương ứng)
Xét hai tam giác vuông IHA và IKA, có:
\(\eqalign{
& \widehat {IHA} = \widehat {IK{\rm{A}}} = 90^\circ \cr
& \widehat {HAI} = \widehat {K{\rm{A}}I}\left( {gt} \right) \cr} \)
AI cạnh huyền chung
Suy ra: ∆IHA = ∆IKA (cạnh huyền, góc nhọn)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông IHB và IKC, có:
\(\widehat {IHB} = \widehat {IKC} = 90^\circ \)
IB = IK (chứng minh trên)
IH = IK (chứng minh trên)
Suy ra: ∆IHB = ∆IKC (cạnh huyền, cạnh góc vuông)
Vậy BH = CK (2 cạnh tương ứng)

