Câu 33: Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB và cung tròn tâm B bán kính BA, chúng cắt nhau ở C và D. Chứng minh rằng:
a) ∆ABC = ∆ABD
b) ∆ACD = ∆BCD
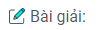
a) Xét ∆ABC và ∆ABD, ta có:
AC = AD (bán kính (A)
AB cạnh chung
BC = BD (bán kính (B)
Suy ra: ∆ABC = ∆BCD(c.c.c)
b) Xét ∆ACD và ∆BCD, ta có ;
Advertisements (Quảng cáo)
AC = BC (bán kính hai đường tròn)
CD cạnh chung
AD = BD (bán kính hai đường tròn)
Suy ra:∆ACD = ∆BCD (c.c.c)
Câu 34: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính bằng BC, vẽ cung tròn tâm C bán kính BA, chúng cắt nhau ở D (D và B nằm khác phía đối với AC). Chứng minh rằng AD // BC.
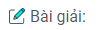
Advertisements (Quảng cáo)
Xét ∆ABC và ∆CDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: \(\Delta ABC{\rm{ }} = {\rm{ }}\Delta CDA{\rm{ }}\left( {c.c.c} \right) \Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\)
Vậy: AD // BC (vì có cặp góc ở vị trí so le trong bằng nhau).
Câu 35: Cho đường thẳng xy, các điểm B và C nằm trên xy, điểm A nằm ngoài xy. Dựa vào bài 34, hãy nêu cách vẽ đường thẳng đi qua A và nằm song song với BC.
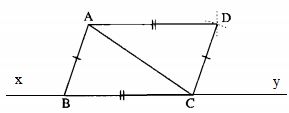
Nói AB, nửa mặt phẳng bờ BC có chứa điểm A.
Vẽ cung tròn tâm A bán kính bằng BC.
Vẽ cung tròn tâm C bán kính bằng AB.
Hai cung tròn cắt nhau tại D.
Kẻ đường thẳng AD ta có AD // xy.

