Câu 45: Vẽ hình theo trình tự sau:
– Vẽ ba điểm không thẳng hàng A, B, C.
– Vẽ đường thẳng \({d_1}\) đi qua B và vuông góc với đường thẳng AC.
– Vẽ đường thẳng \({{\rm{d}}_2}\) đi qua B và song song với AC.
Vì sao \({d_1}\) vuông góc với \({{\rm{d}}_2}\)?
Hình vẽ:
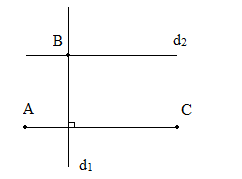
Vì \({{\rm{d}}_1} \bot AC\) và AC // \({{\rm{d}}_2}\) nên \({{\rm{d}}_1} \bot {d_2}\).
Câu 46: Hãy viết trình tự vẽ hình để có hình bên rồi đặt câu hỏi thích hợp:
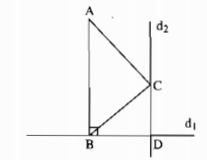
– Vẽ ∆ABC
– Vẽ đường thẳng \({d_1}\) đi qua B và vuông góc với AB
– Vẽ đường thẳng \({d_2}\) đi qua C và vuông góc với AB
– Gọi D là giao điểm của \({d_1}\) và \({d_2}\)
 Tại sao \(\widehat {BDC} = 90^\circ ?\)
Tại sao \(\widehat {BDC} = 90^\circ ?\)
Câu 47: Vẽ hình theo trình tự sau:
– Vẽ tam giác ABC
– Vẽ đường thẳng đi qua A vuông góc với BC tại H
Advertisements (Quảng cáo)
– Vẽ đường thẳng đi qua H vuông góc với AC tại T
– Vẽ đường thẳng đi qua T song song với BC
Trong các hình a, b, c, d dưới đây thì những hình nào vẽ đúng đề bài trên. Hãy điền tên các điểm (theo đề bài) cho các hình vẽ đúng.
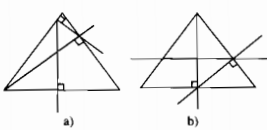
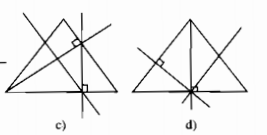
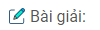
Hình a sai Hình b đúng
Hình c đúng Hình d sai
Tên các điểm được thể hiện trong hình dưới:
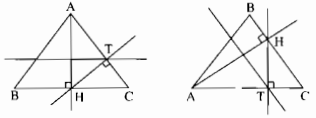
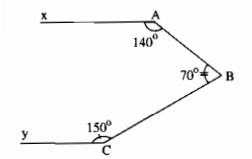
Câu 48: Hình dưới cho biết \(\widehat A = 140^\circ ;\widehat B = 70^\circ ;\widehat C = 150^\circ \)
Chứng minh rằng Ax // Cy
Advertisements (Quảng cáo)
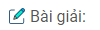
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: \(\widehat {{B_2}} + \widehat {xAB} = 180^\circ \) (hai góc trong cùng phía)
Mà \(\widehat {xAB} = 140^\circ (gt)\)
Suy ra: \(\widehat {{B_2}} = 180^\circ – \widehat {xAB}\)
\( \Rightarrow \) \(\widehat {{B_2}} = 180^\circ – 140^\circ = 40^\circ \)
Mà \(\widehat {{B_1}} + \widehat {{B_2}} = \widehat {ABC}\)
\( \Rightarrow \widehat {{B_1}} = \widehat {ABC} – \widehat {{B_2}}\)
= 70° – 40° = 30° (1)
\(\widehat {yCB} + \widehat {BCy’} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {BCy’} = 180^\circ – \widehat {yCB} = 180^\circ – 150^\circ = 30^\circ (2)\)
Từ (1) và (2) suy ra: \(\widehat {{B_1}} = \widehat {BCy’}\)
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
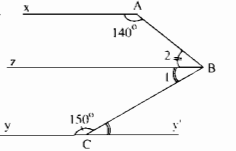
Câu 49: Hình dưới cho biết \(\widehat A + \widehat B + \widehat C = 360^\circ \). Chứng minh rằng Ax // Cy.
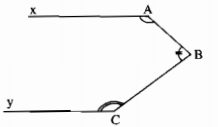
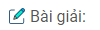
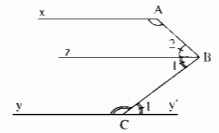
Kẻ Bz // Ax và Cy’ là tia đối của tia Cy.
Ta có: \(\widehat A + \widehat B = 180^\circ \) (hai góc trong cùng phía) (1)
\(\widehat A + \widehat B + \widehat C = 360^\circ \) (gt)
\(\widehat A + \widehat {{B_2}} + \widehat {{B_1}} + \widehat C = 360^\circ (2)\)
Từ (1) và (2) suy ra:
\(\widehat {{B_1}} + \widehat C = 180^\circ \left( 3 \right)\)
\(\widehat C + \widehat {{C_1}} = 180^\circ \) (2 góc kề bù) (4)
Từ (3) và (4) suy ra: \(\widehat {{B_1}} = \widehat {{C_1}}\)
Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra: Ax // Cy.

