Câu 16: Vẽ hình và giới thiệu:
– Hai cặp góc so le trong.
– Bốn cặp góc đồng vị.
– Hai cặp góc so le ngoài.
– Hai cặp góc trong cùng phía.
– Hai cặp góc ngoài cùng phía.
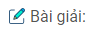
– Hai cặp góc so le trong: \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\)
– Bốn cặp góc đồng vị: \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\); \(\widehat {{A_2}}\) và \(\widehat {{B_2}}\)
\(\widehat {{A_3}}\) và \(\widehat {{B_3}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_4}}\).
– Hai cặp góc so le ngoài: \(\widehat {{A_3}}\) và \(\widehat {{B_1}}\); \(\widehat {{A_2}}\) và \(\widehat {{B_4}}\).
– Hai cặp góc trong cùng phía: \(\widehat {{A_1}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_3}}\).
– Hai cặp góc ngoài cùng phía: \(\widehat {{A_2}}\) và \(\widehat {{B_1}}\); \(\widehat {{A_3}}\) và \(\widehat {{B_4}}\).
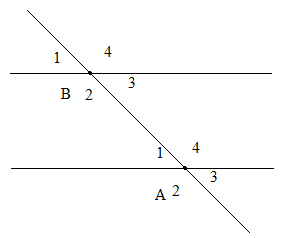
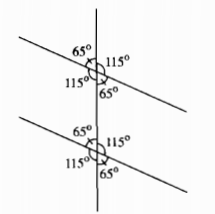
Câu 17: Vẽ lại hình 3 rồi điền tiếp vào hình đó số đo của các góc còn lại.
Câu 18:
a) Vẽ một đường thẳng cắt hai đường thẳng. Trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
b) Vì sao cặp góc so le trong còn lại cũng bằng nhau?
c) Vì sao mỗi cặp góc đồng vị bằng nhau?
Advertisements (Quảng cáo)
d) Vì sao mỗi cặp góc trong cùng phía bù nhau?
e) Vì sao mỗi cặp góc ngoài cùng phía bù nhau?
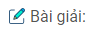
a) Hình vẽ:
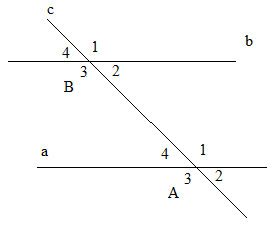
b) Ta có: \(\widehat {{A_4}} = \widehat {{B_2}}\)
\(\widehat {{A_1}} + \widehat {{A_4}} = 180^\circ \) (Hai góc kề bù)
\(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) (Hai góc kề bù)
Suy ra \(\widehat {{A_1}} = \widehat {{B_3}}\)
c) \(\widehat {{A_4}} = \widehat {{B_2}}\)
\(\widehat {{A_2}} = \widehat {{A_4}}\) (Hai góc đối đỉnh)
Suy ra: \(\widehat {{A_2}} = \widehat {{B_2}}\)
Các cặp góc đồng vị khác tương tự.
d) \(\widehat {{A_4}} = \widehat {{B_2}}\)
Advertisements (Quảng cáo)
\(\widehat {{A_1}} + \widehat {{A_4}} = 180^\circ \) (Hai góc kề bù)
Suy ra \(\widehat {{A_1}} + \widehat {{B_2}} = 180^\circ \)
e) \(\widehat {{A_2}} = \widehat {{B_2}}\) (theo câu c)
\(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) (Hai góc kề bù)
Suy ra \(\widehat {{A_1}} + \widehat {{B_2}} = 180^\circ \)
Câu 19: Xem hình 4 rồi điền vào chỗ trống (…) trong các câu sau:
a) \(\widehat {E{\rm{D}}C}\) và \(\widehat {A{\rm{E}}B}\) là cặp góc…….
b) \(\widehat {BE{\rm{D}}}\) và \(\widehat {C{\rm{D}}E}\) là cặp góc…….
c) \(\widehat {C{\rm{D}}E}\) và \(\widehat {BAT}\) là cặp góc…….
d) \(\widehat {{\rm{TAB}}}\) và \(\widehat {DEB}\) là cặp góc…….
e) \(\widehat {{\rm{EAB}}}\) và \(\widehat {ME{\rm{A}}}\) là cặp góc…….
g) Một cặp góc so le trong khác là ……….
h) Một cặp góc đồng vị khác là……..
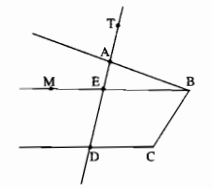
a) \(\widehat {E{\rm{D}}C}\) và \(\widehat {A{\rm{E}}B}\) là cặp góc đồng vị.
b) \(\widehat {BE{\rm{D}}}\) và \(\widehat {C{\rm{D}}E}\) là cặp góc trong cùng phía.
c) \(\widehat {C{\rm{D}}E}\) và \(\widehat {BAT}\) là cặp góc đồng vị.
d) \(\widehat {{\rm{TAB}}}\) và \(\widehat {DEB}\) là cặp góc ngoài cùng phía.
e) \(\widehat {{\rm{EAB}}}\) và \(\widehat {ME{\rm{A}}}\) là cặp góc so le trong.
g) Một cặp góc so le trong khác là \(\widehat {ME{\rm{D}}}\) và \(\widehat {E{\rm{D}}C}\).
h) Một cặp góc đồng vị khác là \(\widehat {{\rm{TAF}}}\) và \(\widehat {A{\rm{D}}C}\).
Câu 20: Trên hình 5 người ta cho biết a // b và \(\widehat {{P_1}} = \widehat {{Q_1}} = 30^\circ \)
a) Viết tên một cặp góc đồng vị khác và nói rõ số đo mỗi góc.
b) Viết tên một cặp góc so le trong và nói rõ số đo mỗi góc.
c) Viết tên một cặp góc trong cùng phía và nói rõ số đo mỗi góc.
d) Viết tên mỗi cặp góc ngoài cùng phía và cho biết tổng số đo hai góc đó.
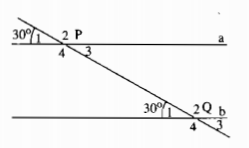
a) Cặp góc đồng vị khác là: \(\widehat {{P_3}} = \widehat {{Q_3}} = 30^\circ \)
b) \(\widehat {{P_3}} = \widehat {{Q_1}} = 30^\circ \)
c) \(\widehat {{P_3}}\) và \(\widehat {{Q_2}}\) là hai góc trong cùng phía.
\(\widehat {{P_3}} = 30^\circ ;\widehat {{Q_2}} = 150^\circ \)
d) \(\widehat {{P_1}}\) và \(\widehat {{Q_4}}\) là hai góc ngoài cùng phía.
\(\widehat {{P_1}} = \widehat {{Q_4}} = 180^\circ \)

