Bài 52: a) Chứng minh rằng nếu ∝ và β khác \({\pi \over 2} + k\pi \,(k \in Z)\) thì:
\(\left\{ \matrix{
\tan \alpha + \tan \beta = {{\sin (\alpha + \beta )} \over {\cos \alpha \cos \beta }} \hfill \cr
\tan \alpha – \tan \beta = {{\sin (\alpha – \beta )} \over {\cos \alpha \cos \beta }} \hfill \cr} \right.\)
b) Chứng minh rằng với mọi ∝ mà cos k∝ ≠ 0 (k = 1, 2, 3, 4, 5, 6, 7, 8) và sin ∝ ≠ 0 thì:
\({1 \over {\cos \alpha \cos 2\alpha }} + {1 \over {\cos 2\alpha \cos 3\alpha }} + … + {1 \over {\cos 7\alpha \cos 8\alpha }} \)
\(= {{\tan 8\alpha – \tan \alpha } \over {\sin \alpha }}\)
Đáp án
a) Ta có:
\(\eqalign{
& \tan \alpha + \tan \beta = {{\sin \alpha } \over {\cos \alpha }} + {{\sin \beta } \over {\cos \beta }} \cr&= {{\sin \alpha \cos \beta + \sin \beta \cos \alpha } \over {\cos \alpha \cos \beta }} \cr
& = {{\sin (\alpha + \beta )} \over {\cos \alpha \cos \beta }} \cr} \)
Tương tự: \(\tan \alpha – \tan \beta = {{\sin (\alpha – \beta )} \over {\cos \alpha \cos \beta }}\)
b) Ta có: \({1 \over {\cos \alpha \cos 2\alpha }} = {{\tan 2\alpha – \tan \alpha } \over {\sin (2\alpha – \alpha )}} = {{\tan 2\alpha – \tan \alpha } \over {\sin \alpha }}\)
Tương tự:
\(\eqalign{
& {1 \over {\cos 2\alpha \cos 3\alpha }} = {{\tan 3\alpha – \tan 2\alpha } \over {\sin \alpha }};… \cr
& {1 \over {\cos 7\alpha \cos 8\alpha }} = {{\tan 8\alpha – \tan 7\alpha } \over {\sin \alpha }} \cr} \)
Advertisements (Quảng cáo)
Do đó: \({1 \over {\cos \alpha \cos 2\alpha }} + {1 \over {\cos 2\alpha \cos 3\alpha }} + … + {1 \over {\cos 7\alpha \cos 8\alpha }} \)
\(= {{\tan 8\alpha – \tan \alpha } \over {\sin \alpha }}\)
Bài 53: Biết cosα +cosβ =a; sinα+sinβ =b (a,b là hằng số và a2 + b2 ≠ 0)
Hãy tính sin(α + β ) theo a và b
Đáp án
Ta có:
\(\left. \matrix{
a = 2\cos {{\alpha + \beta } \over 2}\cos {{\alpha – \beta } \over 2} \hfill \cr
b = 2\sin {{\alpha + \beta } \over 2}\sin {{\alpha – \beta } \over 2} \hfill \cr} \right\} \)
Advertisements (Quảng cáo)
\(\Rightarrow ab = 2\sin (\alpha + \beta )co{s^2}{{\alpha – \beta } \over 2}\)
Mặt khác: \({a^2} + {b^2} = 4{\cos ^2}{{\alpha – \beta } \over 2}\)
Do đó: \(\sin (\alpha + \beta ) = {{2ab} \over {{a^2} + {b^2}}}\)
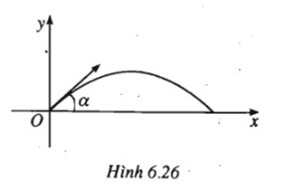
Bài 54: Quỹ đạo của một vật được ném lên từ gốc O, với vận tốc ban đầu là v(m/s) theo phương hợp với trục hoành (nằm ngang) Ox một góc α , \(0 < \alpha < {\pi \over 2}\) là parabol có phương trình :
\(y = – {g \over {2{v^2}{{\cos }^2}\alpha }}{x^2} + (\tan \alpha )x\)
Trong đó g là gia tốc trọng trường (g ≈ 9,8m/s2) (giả sử lực cản của không khí là không đáng kể).
Gọi tầm xa của quỹ đạo là khoảng cách từ O đến giao điểm khác O của quỹ đạo với Ox.
a) Tính tầm xa theo α (và v)
b) Khi v không đổi, α thay đổi trong khoảng \((0,\,{\pi \over 2})\) , hỏi giá trị α nào thì tầm xa của quỹ đạo đạt được giá trị lớn nhất? Tính giá trị đó theo v. Khi v = 80m/s. Hãy tính giá trị lớn nhất đó (chính xác đến hàng đơn vị).
Đáp án
a) Gọi x là tầm xa của quỹ đạo, thì:
\(\left\{ \matrix{
x > 0 \hfill \cr
– {{g{x^2}} \over {2{v^2}{{\cos }^2}\alpha }} + (\tan \alpha )x = 0 \hfill \cr} \right.\)
tức là: \(x = {{2{v^2}\sin \alpha \cos \alpha } \over g} = {{{v^2}} \over g}\sin 2\alpha \)
b) x đạt giá trị lớn nhất khi và chỉ khi \(\sin 2\alpha = 1 \Rightarrow \alpha = {\pi \over 4}\)
Khi đó: \(x = {{{v^2}} \over g}\)
Với \(v = 80m/s\) thì \({{{v^2}} \over g} \approx {{{{80}^2}} \over {9,8}} \approx 653(m)\)

