Bài 43: Xác định các hệ số a, b và c để cho hàm số \(y = ax^2 + bx + c\) đạt giá trị nhỏ nhất bằng \({3 \over 4}\) khi \(x = {1 \over 2}\) và nhận giá trị bằng 1 khi x = 1. Lập bảng biến thiên và vẽ đồ thị của hàm số.
Đáp án
Đặc \(f(x) = ax^2 + bx + c\).
Ta có:
\(\left\{ \matrix{
{x_1} = – {b \over {2a}} \hfill \cr
f({1 \over 2}) = {1 \over 4}a + {1 \over 2}b + c \hfill \cr
f(1) = a + b + c \hfill \cr} \right.\)
Tìm a, b, c thỏa hệ:
\(\left\{ \matrix{
– {b \over {2a}} = {1 \over 2} \hfill \cr
{1 \over 4}a + {1 \over 2}b + c = {3 \over 4} \hfill \cr
a + b + c = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a + b = 0 \hfill \cr
a + 2b + 4 = 3 \hfill \cr
a + b + c = 1 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
a = 1 \hfill \cr
b = – 1 \hfill \cr
c = 1 \hfill \cr} \right.\)
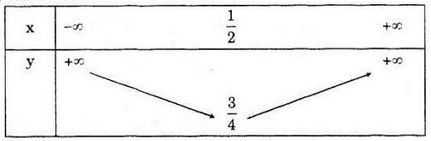
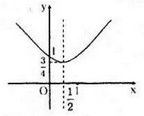
Vậy \(y = x^2 – x + 1\)
Bảng biến thiên:
Đồ thị hàm số:
Bài 44: Vẽ đồ thị của các hàm số sau rồi lập bảng biến thiên của nó
a) \(y = |{3 \over 2}x – 2|\)
b)
\(y = \left\{ \matrix{
2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x < 0 \hfill \cr
{x^2} – x\,\,\,\,\,\,\,;x \ge 0 \hfill \cr} \right.\)
c) \(y = |{1 \over 2}{x^2} + x – {3 \over 2}|\)
d) \(y = x|x| – 2x – 1\)
Đáp án
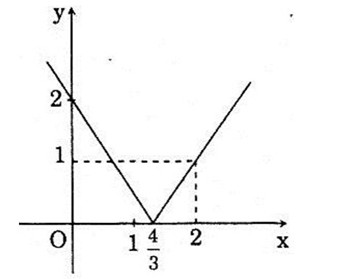
a) Ta có:
Advertisements (Quảng cáo)
\(y = \left\{ \matrix{
{3 \over 2}x – 2\,\,\,\,;x \ge {3 \over 4} \hfill \cr
– {3 \over 2} + 2\,\,\,\,;x < {3 \over 4} \hfill \cr} \right.\)
Đồ thị hàm số:
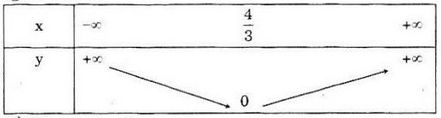
Bảng biến thiên:
b)
Đồ thị hàm số:
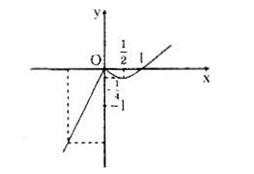
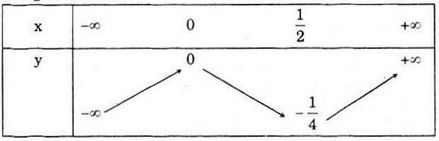
Bảng biến thiên:
c) Ta có:
\(y = \left\{ \matrix{
{1 \over 2}{x^2} + x – {3 \over 2}\,\,\,\,\,\,\,\,\,;\,x \le – 3,x \ge – 1 \hfill \cr
– {1 \over 2}{x^2} – x + {3 \over 2}\,\,\,\,\,\,; – 3 < x < 1 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Đồ thị hàm số:
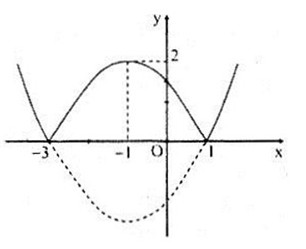
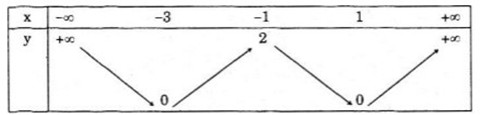
Bảng biến thiên:
d) Ta có:
\(y = \left\{ \matrix{
{x^2} – 2x – 1\,\,\,\,\,;x \ge 0 \hfill \cr
– {(x + 1)^2}\,\,\,\,\,\,\,\,\,;x < 0 \hfill \cr} \right.\)
Đồ thị hàm số:
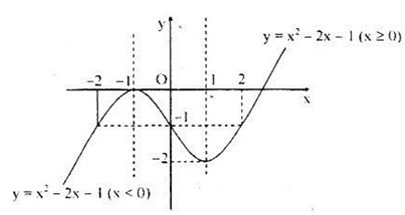
Bảng biến thiên:

Bài 45: Trên hình bên, điểm M chuyển động trên đoạn thẳng AX. Từ M, kẻ đường thẳng song song với AB, cắt một trong ba đoạn thẳng BC, DE, FG tại điểm N. Gọi s là diện tích của miền tô đậm nằm ở bên trái MN. Gọi độ dài đoạn AM là x (0 < x < 9). Khi đó s là một hàm số của biến X. Hãy nêu biểu thức xác định hàm số S(x).
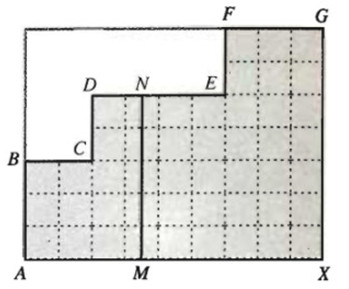
Đáp án
Với x ≤ x < 2 thì S(x) = AM.AB = 3x
Với 2 ≤ x < 6 thì S(x) = AB.BC + MN.DN = 6 + 5(x – 2) = 5x – 4
Với 6 ≤ x ≤ 9 thì S(x) = 6 + 20 +7(x – 6) = 7x – 16
Vậy
\(S(x) = \left\{ \matrix{
3x\,\,\,\,\,\,\,\,\,\,\,;0 \le x 5x – 4\,\,\,\,;2 \le x < 6 \hfill \cr
7x – 16\,\,;6 \le x \le 9 \hfill \cr} \right.\)
Bài 46: Khi một con tàu vũ trụ được phóng lên Mặt Trăng, trước hết nó sẽ bay vòng quanh Trái Đất. Sau đó, đến một thời điểm thích hợp, động cơ bắt đầu hoạt động đưa con tàu bay theo quỹ đạo là một nhánh hình parabol lên Mặt Trăng (trong hệ tọa độ Oxy như hình vẽ bên, X và y tính bằng nghìn kilômét). Biết rằng khi động cơ bắt đầu hoạt động, x= 0 thì y = -7. Sau đó y = -4 khi x = 10 và y = 5 khi x = 20.
a) Tìm hàm số có đồ thị là nhánh parabol nói trên
b) Theo lịch trình, đế đến được Mặt Trăng, con tàu phải đi qua điểm (100; V) với \(y = 294 ± 1,5\). Hỏi điều kiện đó có được thỏa màn hay không?
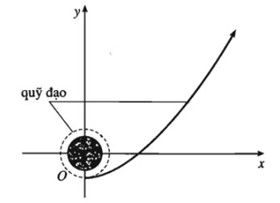
Đáp án
a) Gọi hàm bậc hai cần tìm là \(y = f(x) = ax^2 + bx + c\)
Theo đề bài ta có:
\(\left\{ \matrix{
f(0) = – 7 \hfill \cr
f(10) = – 4 \hfill \cr
f(20) = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
c = – 7 \hfill \cr
100a + 10b + c = – 4 \hfill \cr
400a + 20b + c = 5 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
a = 0,03 \hfill \cr
b = 0 \hfill \cr
c = – 7 \hfill \cr} \right.\)
Vậy: \(y = 0,03x^2– 7\)
b) Theo điều kiện khi \(x = 100\) thì \(y = 294 ± 1,5\)
Tức \(294 – 1,5 \le y \le 294 + 1,5\)
\(⇔ y ∈ [292,5; 295,5]\)
Ta có: \(f(100) = 0,03.100^2– 7 = 293\) (thỏa mãn điều kiện)

