Bài 20: Có phải mọi đường thẳng trong mặt phẳng toạ độ đều là đồ thị của một hàm số nào đó không ? Vì sao?
Không phải.
Vì mỗi đường thẳng trong mặt phẳng tọa độ đều là đồ thị của một hàm số nào đó. Với các đường thẳng cùng phương với trục tung (có phương trình x = a) không là đồ thị của một hàm số.
Bài 21: a) Tìm hàm số y = f(x), biết rằng đồ thị của nó là đường thẳng đi qua điểm (-2 ; 5) và có hệ số góc bằng -1,5 ;
b) Vẽ đồ thị của hàm số tìm được.
a) Đồ thị hàm số y = f(x) là đườnng thẳng nên có dạng \(y = ax + b\) với \(a = -1,5\)
Do đó: \(y = -1,5 x + b\)
Advertisements (Quảng cáo)
Đường thẳng đi qua điểm \((-2; 5)\) nên:
\(5 = (-1,5).(-2) + b ⇒ b = 2\)
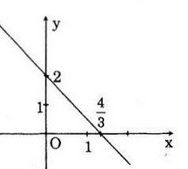
Vậy d: \(y = -1,5x + 2\)
b) Đồ thị của hàm số
Advertisements (Quảng cáo)
Bài 22: Tìm bốn hàm số bậc nhất của đồ thị là bốn đường thẳng đôi một cắt nhau tại bốn đỉnh của một hình vuông nhận gốc O làm tâm đối xứng, biết rằng một đỉnh của hình vuông này là A (3 ; 0).
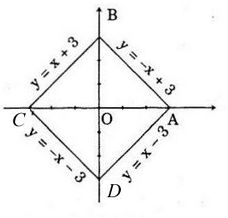
Vì O là tâm đối xứng của hình vuông và có đỉnh \(A(3; 0)\) nên các đỉnh còn lại của hình vuông là: \(B(0; 3); C(-3; 0); D(0; -3)\)
Đường thẳng đi qua hai điểm A, B có dạng \(y = ax + b\)
\(A(3; 0); B(0; 3)\) nằm trên đường thẳng nên:
\(\left\{ \matrix{
0 = 3a + b \hfill \cr
3 = b \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = – 1 \hfill \cr
b = 3 \hfill \cr} \right.\)
Vậy AB: \(y= -x + 3\)
Tương tự:
BC: \(y = x + 3\)
CD: \(y = -x – 3\)
DA: \(y = x – 3\)

