Bài 39: Với mỗi câu sau đây. Hãy chọn phần kết luận mà em cho là đúng:
a) Trên khoảng (-1; 1), hàm số y = -2x + 5
(A) Đồng biến
(B) Nghịch biến;
(C) Cả kết luận (A) và (B) đều sai.
b) Trên khoảng (0; 1), hàm số y = x2 + 2x – 3
(A) Đồng biến
(B) Nghịch biến;
(C) Cả kết luận (A) và (B) đều sai.
c) Trên khoảng (-2; 1) hàm số y = x2 + 2x – 3
(A) Đồng biến
(B) Nghịch biến;
(C) Cả kết luận (A) và (B) đều sai.
Đáp án
a) Chọn (B)
b) Chọn (A)
c) Chọn (C)
Bài 40: a) Tìm các hàm số lẻ trong các hàm số bậc nhất \(y = ax + b\).
b) Tìm các hàm số chẵn trong các hàm số bậc hai \(y = ax^2 + bx + c\).
Đáp án
a) Đặc \(f(x) = ax + b (a ≠ 0)\)
Advertisements (Quảng cáo)
\(y = f(x)\) là hàm số lẻ khi \(f(-x) = -f(x); ∀x ∈\mathbb R\)
\(⇔ -ax + b = -(ax + b) ⇔ b = 0\)
Với \(a ≠ 0, b = 0\) thì \(y = ax + b\) là hàm số lẻ.
b) Đặc \(f(x) = ax^2+ bx + c (a ≠ 0)\)
\(y = f(x)\) là hàm số chẵn khi \(f(-x) = f(x); ∀x ∈\mathbb R\)
\(⇔ ax^2- bx + c = ax^2+ bx + c ; ∀x ∈\mathbb R\)
\(⇔ 2bx = 0; ∀x ∈\mathbb R⇔ b = 0\)
Vậy với \(a ≠ 0; b = 0; c\) tùy ý thì hàm số \(y = ax^2+ bx + c\) là hàm số chẵn
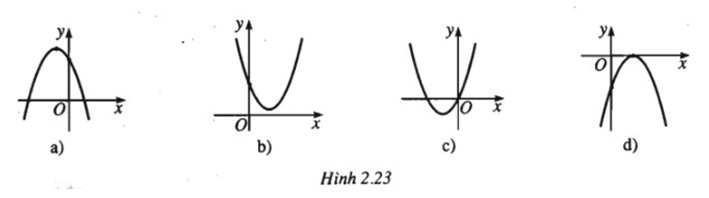
Bài 41: Dựa vào đồ thị của hàm số \(y = ax^2 + bx + c\). Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:
Đáp án
a) Parabol (P1) có bề lõm quay xuống nên a < 0
(P1) cắt trục Oy tại điểm có tung độ dương nên c = f(0) > 0
Hoành độ đỉnh \({x_0} = – {b \over {2a}} < 0 \Rightarrow b < 0\) (do a <0)
Advertisements (Quảng cáo)
b) Parabol (P2) có bề lõm quay lên nên a > 0
(P1) cắt trục Oy tại điểm có tung độ dương nên c = f(0) > 0
Hoành độ đỉnh \({x_0} = – {b \over {2a}}\) > 0 ⇒ b < 0 (do a >0)
c) Parabol (P3) có bề lõm quay lên nên a > 0
(P3) đi qua gốc O nên c = 0
Hoành độ đỉnh \({x_0} = – {b \over {2a}}\) < 0 ⇒ b > 0 (do a >0)
d) Parabol (P3) có bề lõm quay xuống nên a < 0
(P3) cắt trục Oy tại điểm có tung độ âm nên c < 0
Hoành độ đỉnh \({x_0} = – {b \over {2a}}\) > 0 ⇒ b > 0 (do a < 0)
Bài 42: Trong mỗi trường hợp cho dưới đây, hãy vẽ đồ thị hàm số của các hàm số trên cùng một hệ trục tọa độ rồi xác định tọa độ giao điểm của chúng.
a) \(y = x – 1\) và \(y = x^2 – 2x – 1\);
b) \(y = -x + 3\) và \(y = -x^2 – 4x + 1\);
c) \(y = 2x – 5\) và \(y = x^2 – 4x – 1\).
Đáp án
a) Đường thẳng d: \(y = x – 1\) qua \(A(0; -1); B(1; 0)\)
Parabol (P): \(y = x^2– 2x – 1\) có đỉnh \(S(1; -2)\)
Phương trình hoành độ giao điểm của d và (P) là:
\(x^2 – 2x – 1 = x – 1 ⇔ x^2 – 3x = 0\)
\( \Leftrightarrow \left[ \matrix{
x = 0\,\,(y = – 1) \hfill \cr
x = 3\,\,(y = 2) \hfill \cr} \right.\)
Giao điểm của d và (P) là: \(A(0, -1)\) và \(C(3, 2)\)
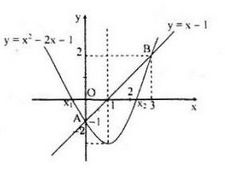
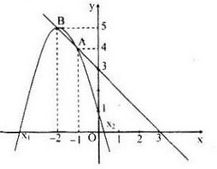
b) Đường thẳng d: \(y = -x + 3\) qua \(A(0, 3); B(3, 0)\)
Parabol (P): \(y = -x^2 – 4x + 1\) có đỉnh \(S(-2, 5)\)
Phương trình hoành độ giao điểm của và (P) là:
\(\eqalign{
& – {x^2} – 4x + 1 = – x + 3 \cr
& \Leftrightarrow {x^2} + 3x + 2 = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = – 1\,\,\,\,(y = 4) \hfill \cr
x = – 2\,\,\,\,(y = 5) \hfill \cr} \right. \cr} \)
Giao điểm của d và (P) là \((-1, 4)\) và \((-2, 5)\)
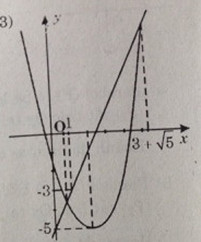
c) Đường thẳng d: \(y = 2x – 5\) đi qua \(A(0, -5); B(1, -3)\)
Parabol (P): \(y = x^2 – 4x – 1\) có đỉnh \(S(2, -5)\)
Phương trình hoành độ giao điểm của và (P) là:
\(\eqalign{
& {x^2} – 4x – 1 = 2x – 5 \Leftrightarrow {x^2} – 6x + 4 = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 3 – \sqrt 5 \,\,\,\,\,\,\,\,(y = 1 – 2\sqrt 5 ) \hfill \cr
x = 3 + \sqrt 5 \,\,\,\,\,\,\,\,\,(y = 1 + 2\sqrt 5 ) \hfill \cr} \right. \cr} \)
Giao điểm của (P) và d là: \((3 – \sqrt 5 ,\,1 – 2\sqrt 5 );\,(3 + \sqrt 5 ,\,1 + 2\sqrt 5 )\)