Câu C1: Từ thí nghiệm trên , rút kinh nghiệm gì ?
Giải :
Từ thí nghiệm trên , rút ra được kết luận: Hợp lực \(\overrightarrow F \) của hai lực đồng quy \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng tác dụng vào một vật là lực được xác định bởi phép cộng vectơ \(\overrightarrow F =\overrightarrow {{F_1}} \,+\overrightarrow {{F_2}} \) có nghĩa là \(\overrightarrow F \) là vec tơ đường chéo của hình bình hành có hai cạnh là \({\overrightarrow F _1}\) và \(\overrightarrow {{F_2}} \).
Câu C2: Nếu phải tổng hợp nhiều lực đồng quy thì vận dụng quy tắc hình bình hành như thế nào ?
Giải :
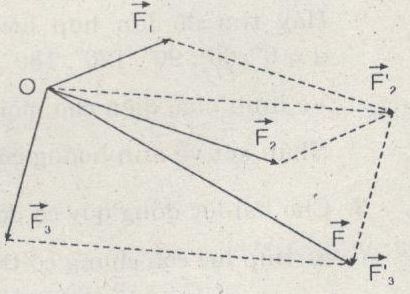
Nếu phải tổng hợp nhiều lực đồng quy (\(\overrightarrow F =\overrightarrow {{F_1}} +\overrightarrow {{F_2}} +\overrightarrow {{F_3}} \) chẳng hạn) thì áp dụng quy tắc đa giác để xác định hợp lực
Bài 1: Gọi \({F_1};{F_2}\) là độ lớn của hai lực thành phần, F là độ lớn hợp lực của chúng. Câu nào sau đây là đúng ?
A.Trong mọi trường hợp F luôn luôn lớn hơn cả F1 và F2
B. F không bao giờ nhỏ hơn cả F1 và F2
C. Trong mọi trường hợp, F thõa mãn : \(\left| {{F_1} – {F_2}} \right| \le F \le {F_1} + {F_2}\)
Advertisements (Quảng cáo)
D. F không bao giờ bằng F1 hoặc F2
Giải :
Chọn C. ( Vì \(\overrightarrow F = \,\,\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) nên thỏa mãn \(\left| {{F_1} – {F_2}} \right| < F < {F_1} + {F_2})\)
Bài 2: Cho hai lực đồng quy có độ lớn : \({F_1} = {F_2} = 20N\)
Hãy tìm độ lớn hợp lực của hai lực khi chúng hợp lực với nhau một góc \(\alpha = {0^0},{60^0},{90^0},{120^0},{180^0}.\)
Vẽ hình biểu diễn cho mỗi trường hợp.
Advertisements (Quảng cáo)
Nhận xét về ảnh hưởng của góc \(\alpha \) đối với độ lớn của hợp lực
Giải
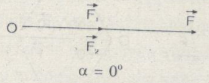
\(F = {F_1} + {F_2} = 40\,N\)
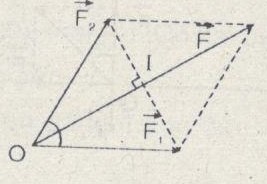
\(\eqalign{ & F = 2.OI = 2.{F_2}.\cos {\alpha \over 2} \cr & \;\;\;\;= 2.20.{{\sqrt 3 } \over 2} = 20\sqrt 3 \,N \cr} \)
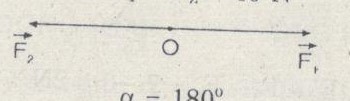
\(\alpha = {180^0}\)
\(F = 0\;N\)
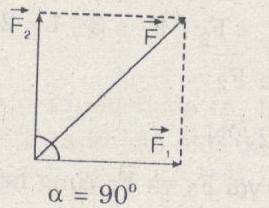
\(\alpha = {90^0}\)
\(F = {F_1}\sqrt 2 = 20\sqrt 2 \,(N)\)
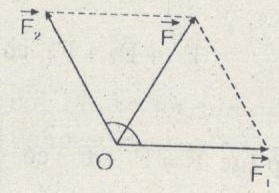
\(\eqalign{ & \alpha = {120^0} \cr & F = {F_1} = {F_2} = 20\,N \cr} \)
Nhận xét : Góc \(\alpha \) càng nhỏ thì hợp lực càng lớn

