Bài 3: Cho hai lực đồng quy có độ lớn \({F_1} = 16\,N\) và \({F_2} = 12\,N\)
a) Hợp lực của chúng có thể có độ lớn 30 N hoặc 3,5 N được không ?
b) Cho biết độ lớn của hợp lực F = 20 N . Hãy tím góc giữa lực \(\overrightarrow {{F_1}} \,và\,\overrightarrow {{F_2}} \)
Giải
\({F_1} = 16\,N\,;{F_2} = 12\,N\)
a) Hợp lực \(\overrightarrow {{F_1}} \) có độ lớn \(4 \le F \le 28\) (N) do đó F không thể lấy giá trị 30 (N) hoặc 3,5 (N) được.
b)
\(\eqalign{ & \overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \cr & F = 20\,N\,;\,{F_1} = 16N\,;{F_2} = 12\,N \cr} \)
=>\(\left\{ \matrix{ {F^2} = F_1^2 + F_2^2\text{ tam giác lực là tam giác vuông }\hfill \cr Với\,\,\overrightarrow {{F_1}} \, \bot \,\overrightarrow {{F_2}} \hfill \cr} \right.\)
Vậy góc \(\alpha = (\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = {90^0}.\)
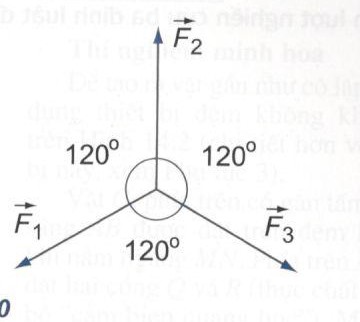
Bài 4: Cho ba lực đồng quy cùng nằm trong một mặt phẳng, có độ lớn bằng nhau và từng đôi một làm thành góc \({120^0}\)(hình 13.10).Tìm hợp lực của chúng.
Giải
Advertisements (Quảng cáo)
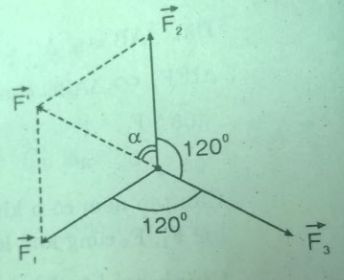
\(\overrightarrow {F\,\,\,} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \,\, = \,\overrightarrow {{F’}\,} + {\overrightarrow F _3} = \overrightarrow 0 \)
Hình bình hành OF1F’F2 là hình thoi gồm hai tam giác đều
nên F’ = F1 = F2 = F3 và \(\alpha = {60^0}\)
\(\overrightarrow {{F’}} \,\) nằm tronh mặt phẳng chứa \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)
\(\eqalign{ & = > \,\overrightarrow {F’} \,\text{ và }\,\overrightarrow {F_3} \text{ trực đối} \cr & = > \overrightarrow F = \overrightarrow {F’} + \overrightarrow {{F_3}} = \overrightarrow 0 \cr} \)
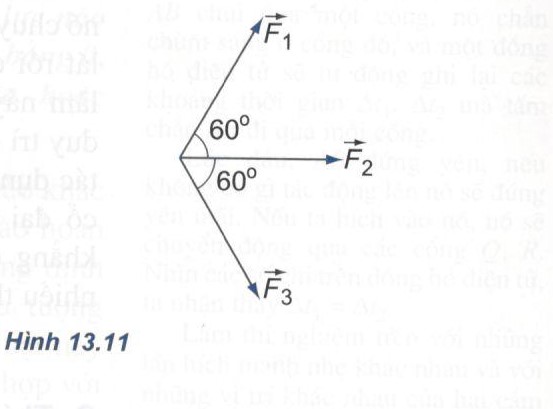
Bài 5: Hãy dùng quy tắc hình bình hành và quy tắc đa giác để tìm hợp lực của ba lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) và \(\overrightarrow {{F_3}} \) có độ lớn bằng nhau và nằm trong cùng một mặt phẳng. Biết rằng lực \(\overrightarrow {{F_2}} \) làm thành với hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_3}} \) những góc đều là 600 (Hình 13.11).
Giải :
Advertisements (Quảng cáo)
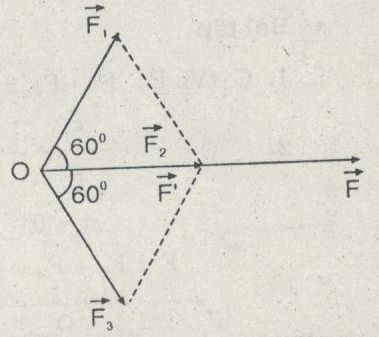
\(\overrightarrow F = \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_1}} = \overrightarrow {{F_2}} + \overrightarrow {F’} = 2\overrightarrow {{F_2}} \)
Tương tự như bài 4, \(\overrightarrow {F’} = \overrightarrow {{F_2}} \to \overrightarrow F = 2\overrightarrow {{F_2}} \)
Bài 6: Tìm hợp lực của bốn lực đồng quy trong Hình 13.12.
Biết \({F_1} = 5N,{F_2} = 3N,{F_3} = 7N\,,{F_4} = 1N\)
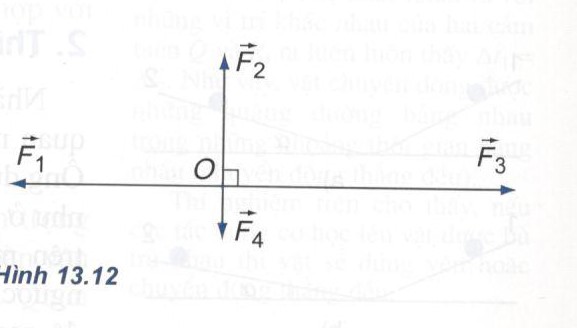
Giải
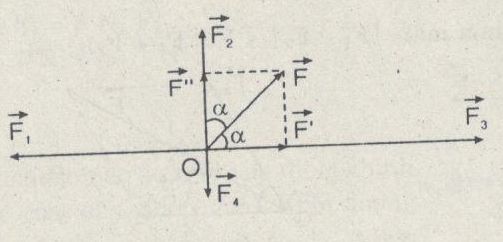
\(\eqalign{ & \overrightarrow {F’} = \overrightarrow {{F_1}} + \overrightarrow {{F_3}} \text{ có }\cr&\left\{ \matrix{ độ\, \text{lớn }F’ = {F_3} – {F_1} = 7 – 5 = 2N \hfill \cr \text{ chiều của }\overrightarrow {{F_3}} \hfill \cr} \right. \cr & \overrightarrow {F”} + \overrightarrow {{F_2}} + \overrightarrow {{F_4}} \text{ có }\cr&\left\{ \matrix{ độ\, \text{lớn }F” = {F_2} – {F_4} = 3 – 1 = 2N \hfill \cr \text{ chiều của }\overrightarrow {{F_2}} \hfill \cr} \right. \cr} \)
\(\text{ Hợp lực }\overrightarrow {F\,} = \overrightarrow {F’} + \overrightarrow {F”} \text{ có }\)
\(\left\{ \matrix{ độ\,\text{lớn }\,F = 2\sqrt 2 N \hfill \cr \text{hướng hợp với }\overrightarrow {{F_3}} \,\text{và}\,\overrightarrow {{F_2}} \text{ cùng một góc }\alpha = {45^0} \hfill \cr} \right.\)
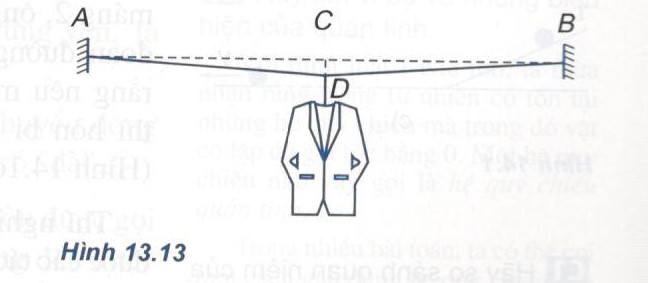
Bài 7: Một chiếc mắc áo treo vào điểm chính giữa của dây thép AB. Khối lượng tổng cộng của mắc áo và áo là 3 kg (Hình 13.13).
Biết AB = 4m ; CD =10 cm
Tính lực kéo mỗi nửa sợi dây.
Giải :
∆DAB cân tại D có đường trung trực DC trùng với giá của trọng lực \(\overrightarrow P \) tác dụng lên mắc và áo nên nếu phân tích \(\overrightarrow P = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) như hình vẽ thì hình bình hành là hình thoi và \({F_1} = {F_2} = {{DI} \over {\sin \alpha }}\,;\) với \(DI = {P \over 2} = {{mg} \over 2};\) \(\sin \alpha = {{CD} \over {AD}} = {{CD} \over {\sqrt {A{C^2} + C{D^2}} }}\)
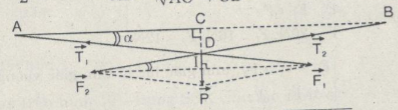
Ta được : \({F_1} = {F_2} = {{mg\sqrt {A{C^2} + C{D^2}} } \over {2CD}} = {{3.9,8\sqrt {{2^2} + 0,{1^2}} } \over {2.0,1}} \approx 294,4(N)\)
Chất điểm D cân bằng dưới tác dụng của 4 lực đôi một cùng phương ngược chiều và \({F_1} = {F_2}\) nên \({T_1} = {T_2} = {F_1} = {F_2} = 294,4\,N\)
Vậy lực căng mỗi nhánh dây là 294,4 N

