Trang Chủ Bài tập SGK lớp 10 Bài tập Vật Lý 10 Nâng cao

Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 16, 17 Sách Vật lý 10 Nâng cao – Bài 2 Vận tốc trong chuyển động thẳng, chuyển động thẳng đều.

Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 16, 17 SGK Vật lý 10 Nâng cao. Bài 2 Vận tốc trong chuyển động thẳng, chuyển động thẳng đều. Chọn câu sai; Bài 2 Vận tốc trong chuyển động thẳng, chuyển động thẳng đều.

Bài 1: Chọn câu sai

A. Vectơ độ dời là một vectơ nối vị trí đầu và vị trí cuối của chất điểm chuyển động

B. Vectơ độ dời có độ lớn luôn luôn bằng quãng đường đi được của chất điểm

C. Chất điểm đi trên một đường thẳng rồi quay về vị trí ban đầu thì có độ dời bằng 0

D. Độ dời có thể dương hoặc là âm

Giải :

Đáp án B. Vectơ độ dời có độ lớn luôn luôn bằng quãng đường đi được của chất điểm

Bài 2: Câu nào sau đây đúng

A. Độ lớn của vận tốc trung bình bằng tốc độ trung bình

B. Độ lớn của vận tốc tức thời bằng tốc độ tức thời

C. Khi chất điểm chuyển động thẳng chỉ một chiều thì bao giờ vận tốc trung bình tốc độ trung bình

D. Vận tốc tức thời cho ta biết theo thời gian , do đó bao giờ cũng có giá trị dương

Giải:

Chọn đáp án B

A. Sai. (Độ lớn của vận tốc trung bình chỉ bằng tốc độ trung bình khi chất điểm chuyển động thẳng theo một chiều nhất định)

B. Đúng (Vì trong ∆t rất nhỏ, chất điểm không đổi chiều chuyển động )

C. Sai. (Chỉ khi chất điểm chuyển động thẳng theo một chiều dương thì mới có vận tốc trung bình = tốc độ trung bình)

D. Sai. (Nếu chất điểm chuyển động ngược chiều dương thì v < 0 ; mặc dù \(\overrightarrow v \) vẫn chỉ chiều chuyển động )

Bài 3: Câu nào sau đây sai

A. Đồ thị vận tốc theo thời gian chuyển động thẳng đều là một đường song song với trục hoành Qt

B. Trong chuyển động thẳng đều , đồ thị thời gian của tọa độ và của vận tốc đều là nhungữ đường thẳng

C. Đồ thị tọa độ theo thời gian chuyển động bao giờ cũng là một đường thẳng

D. Đồ thị theo thời gian của chuyển động thẳng đều là một đường thẳng xiên góc

Giải:

Chọn đáp án C

Đồ thị tọa độ-thời gian của chuyển động thẳng nhanh dần, chậm dần là một đường cong.

Bài 4: Một người đi bộ trên đường thẳng. Cứ đi được 10m thì người đó nhìn đồng hồ đo khoảng thời gian đã đi. Kết quả đo độ dời và thời gian thực hiện được ghi trong bảng sau:

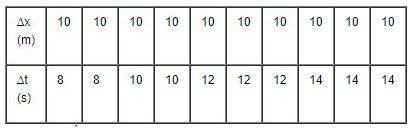
a) Tính vận tốc trung bình cho từng đoạn đường 10 m

b) Vận tốc trung bình cho cả quãng đường đi là bao nhiêu? So sánh giá trị trung bình trên mỗi đoạn đường 10m a) Tính vận tốc trung bình cho từng đoạn đường 10m

Advertisements (Quảng cáo)

Giải:

Chọn chiều dương là chiều chuyển động để ∆x > 0; v_tb > 0

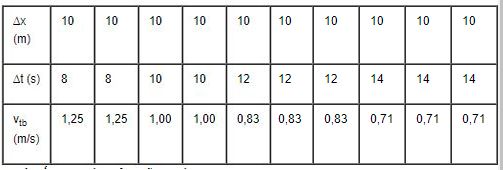
b) Vận tốc trung bình của quãng đường

\({v_{tb\,\,}} = \,{S \over t} = {{10.10} \over {2.8 + 2.10 + 3.12 + 3.14}} = 0,88\,(m/s)\)

Giá trị trung bình của các vận tốc trung bình trên mỗi đoạn 10 m:

\(\overline {v\,} {\rm{ = }}{{{\rm{2}}{\rm{.1,25 + 2}}{\rm{.1,00 + 3}}{\rm{.0,83 + 3}}{\rm{.0,71}}} \over {{\rm{10}}}}{\rm{ = 0,91}}\,{\rm{(m/s)}}\)

Như vậy: \({v_{tb\,\,}} \ne \overline v \)

Bài 5: Hai người đi bộ cùng chiều trên một đường thẳng. Người thứ nhất đi với vận tốc không đổi bằng 0,9 m/s. Người thứ hai đi với vận tốc không đổi bằng 1,9 m/s. Biết hai người cùng xuất phát cùng một vị trí.

a) Nếu người thứ hai đi không nghỉ thì sau bao lâu sẽ đến một địa điểm cách nơi xuất phát 780m ?

b) Người thứ hai đi được một đoạn thì dừng lại, sau 5,50 min thì người thứ nhất đến. Hỏi vị trí đó cách nơi xuất phát bao xa ?

Giải

Chọn chiều (+) là chiều chuyển động , gốc O ≡ vị trị xuất phát, gốc thời gian là lúc xuát phát

a) Phương trình chuyển động của người II:

\(\eqalign{
& {x_2} = 1,9t\,(s;m)\, \Rightarrow \,\,t = {{{x_2}} \over {1,9}} = {{780} \over {1,9}} = \,410,5\,\,(s) \cr
& \,\,t \approx \,6\text{ min }51\,s \cr} \)

b) Phương trình chuyển động của người thứ I :

\({x_1} = 0,9t\,\left( {s;m} \right)\)

Đổi 5,50 min = 330 (s)

Theo đề bài , ta có phương trình

Advertisements (Quảng cáo)

\(1,9(t – 330) = 0,9t\)

⟹ Thời điểm người I đến vị trí đó : t = 627 (s)

Vị trí phải tìm : x = 0,9 . 627 = 564,3 (m)

Bài 6: Một ô tô chạy trên đường thẳng. Trên nửa đầu của đường đi, ô tô chạy với vận tốc không đổi, 50 km/h. Trên quãng đường còn lại, ô tô chạy với vận tốc không đổi bằng 60 km/h.

Tính vận tốc trung bình của ô tô trên cả quãng đường.

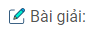
Đặt AB = S thì \(AC = CB = {S \over 2}\)

Chọn hệ tọa độ như hình trên , gốc thời gian \(({t_0}\, = 0)\) là lúc xuất phát từ A thì :

\(t = \,{t_1} + {t_2} = {{AC} \over {{v_1}}} + {{CB} \over {{v_2}}} = {S \over {2.50}} + {S \over {2.60}} = {{11S} \over {600}}\)

Vận tốc trung bình trên quãng đường AB :

\({v_{tb}} = {S \over t} = {S \over {{{11S} \over {600}}}} = 54,55\,(m/s)\)

Bài 7: Đồ thị tọa độ theo thời gian của một người chạy trên một đường thẳng được biểu diễn trên hình sau . Hãy tính độ dời và vận tốc trung bình của người đó

a) Trong khoảng thời gian 10 min đầu tiên

b) Trong khoảng thời gian từ \({t_{1\,}} = 10\) min đến \({t_2} = 30\)

c) Trong cả quãng đường chạy 4,5 km

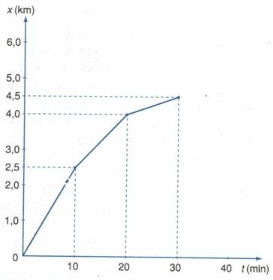
Giải:

a) Trong

\(\Delta {t_1} = 10\min \left\{ \matrix{
\Delta {x_1} = 2,5km \hfill \cr
{v_{t{b_1}}} = {{\Delta {x_1}} \over {\Delta {t_1}}} = {{2,5} \over {10}} = 0,25(km/\min ) \hfill \cr} \right.\)

b) Trong \(\Delta {t_2} = {t_2} – {t_1} = 20 – 10 = 10\min \)

\(\left\{ \matrix{
\Delta {x_2} = 4,0 – 2,5 = 1,5(km) \hfill \cr
{v_{t{b_2}}} = {{\Delta {x_2}} \over {\Delta {t_2}}} = {{1,5} \over {10}} = 0,15(km/\min ) \hfill \cr} \right.\)

c) Trong

\(\Delta {t_1} = 30\min :\left\{ \matrix{
\Delta x = 4,5km \hfill \cr
{v_{tb}} = {{\Delta x} \over {\Delta t}} = {{4,5} \over {30}} = 0,15(km/\min ) \hfill \cr} \right.\)

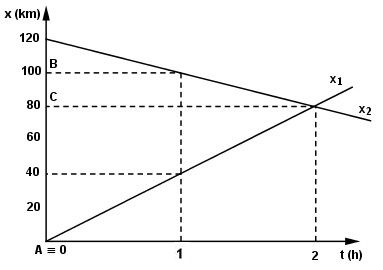
Bài 8: Hai xe chạy ngược chiều đến gặp nhau . Cùng khởi hành một lúc từ hai địa điểm A và B cách nhau 120km. Vận tốc của xe đi từ A là 40 km/h, của xe B là 20 km/h. Coi chuyển động của các xe như chuyển động của xe như chuyển động của các chất điểm trên đường thẳng.

a) Viết phương trình chuyển động của từng xe. Từ đó tính thời điểm và vị trí hai xe gặp nhau

b) Giải bài toán trên bằng đồ thị

Giải:

Chọn trục Ox ≡ đường thẳng AB ; chiều dương hướng từ A đến B

Gốc thời gian \(({t_0} = 0)\)lúc hai xe cùng khởi hành

a) Dạng phương trình chuyển động : \(x = {x_0} + vt\)

– Với xe đi từ A : \({x_{10}} = 0\,;{v_1} = 40\,\left( {km/h} \right)\,\,(\overrightarrow {{v_1}} \) cùng chiều dương )

Phương trình chuyển động : \({x_1} = 40t\,(h;km)\)

-Với xe đi từ B : \({x_{20}} = 120km\,({x_{20}} > 0\) vì vec tơ \(\overrightarrow {OB} \) cùng chiều dương )

\({v_2} = – 20\,(km/h)\,({v_2} < 0\) vì vectơ \(\overrightarrow {{v_2}} \) ngược chiều dương )

Phương trình chuyển động : \({x_2} = 120 – 20t\,(h;km)\)

– Khi hai xe gặp nhau tại C thì

\(\eqalign{ & {x_C} = {x_1} = {x_2} \cr& 40t = 120 – 20t \cr} \)

Thời điểm gặp nhau : t = 2 (h)

Vị trí gặp nhau : \({x_C} = 40.2 = 80(km)\)

b) Sau 2h chuyển động thì hai xe gặp nhau tại C cách A = 80 km

Hai đường thẳng \({x_1}(t)\) và \({x_2}(t)\) cắt nhau tại điểm (2;80)

– Thời điểm gặp nhau lúc 2 h

– Vị trí gặp nhau \({x_C} = 40.2 = 80\,(km)\)

BÀI VIẾT LIÊN QUAN

XEM THEO LỚP