Bài 4: Cho tam giác ABC.
a) Tam giác ABC có tính chất gì nếu \({a^2} = {{{b^3} + {c^3} – {a^3}} \over {b + c – a}}\)?
b) Biết \({2 \over {{h_a}}} = {1 \over {{h_b}}} + {1 \over {{h_c}}}\) , chứng minh rằng \(2\sin A = \sin B + \sin C\) .
Giải: a) Ta có
\(\eqalign{
& {a^2} = {{{b^3} + {c^3} – {a^3}} \over {b + c – a}}\cr& \Leftrightarrow \,\,{a^2}b + {a^2}c – {a^3} = {b^3} + {c^3} – {a^3} \cr
& \Leftrightarrow \,\,{a^2}\left( {b + c} \right) = \left( {b + c} \right)\left( {{b^2} – bc + {c^2}} \right) \cr
& \Leftrightarrow \,\,{a^2} = {b^2} + {c^2} – bc \cr} \)
Áp dụng định lí cosin ta có \({a^2} = {b^2} + {c^2} – 2bc\cos A\) .
Do đó \(\cos A = {1 \over 2}\,\, \Leftrightarrow \,\,\widehat A = {60^0}\).
Vậy tam giác ABC có góc A bằng \({60^0}\) .
b) Ta có \(S = {1 \over 2}a{h_a}\,\, \Rightarrow \,\,{h_a} = {{2S} \over a}\,\,\,\,;\,\,\,S = {1 \over 2}b{h_b}\)
\(\Rightarrow \,\,{h_b} = {{2S} \over b}\,\,;\,\,{h_c} = {{2S} \over c}\) .
Do đó
\(\eqalign{
& {2 \over {{h_a}}} = {1 \over {{h_b}}} + {1 \over {{h_c}}}\,\,\, \Leftrightarrow \,\,2a = b + c \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,2.2R\sin A = 2R\sin B + 2R\sin C \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,2\sin A = \sin B + \sin C \cr} \)
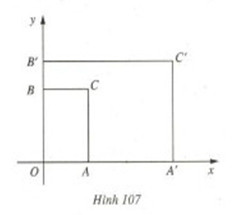
Bài 5: Trong mặt phẳng tọa độ Oxy cho hai hình chữ nhật OACB và OA’C’B’ như hình 107. Biết \(A(a\,;\,0)\,,\,{A’}({a’}\,;\,0)\,,\,B(0\,;\,b)\,,\,{B’}(0\,;\,{b’}\,)\,\) (a, a’, b, b; là những số dương, \(a\, \ne {a’}\,,\,b\, \ne \,{b’}\)).
a) Viết phương trình các đường thẳng AB’ và A’B.
b) Tìm liện hệ giữa để hai đường thẳng AB’ và A’B cắt nhau. Khi đó hãy tìm tọa độ giao điểm I của hai đường thẳng đó.
c) Chứng minh rằng ba điểm I, C, C’ thẳng hàng.
d) Với điều kiện nào của a, a’, b, b’; thì C là trung điểm của IC’?
Giải
Advertisements (Quảng cáo)
a) Áp dụng phương trình đường thẳng theo đoạn chắn, ta có
\(A{B’}:\,\,{x \over a} + {y \over {{b’}}} = 1\,\,;\,\,\,\,{A’}B:\,\,{x \over {{a’}}} + {y \over b} = 1\)
b) A’B và AB’ cắt nhau \( \Leftrightarrow \,\,{a \over {{a’}}} \ne {{{b’}} \over b}\,\, \Leftrightarrow \,\,ab – {a’}{b’} \ne 0\) . Tọa độ giao điểm I của A’B và AB’ là nghiệm của hệ phương trình:
\(\left\{ \matrix{
{b’}x + ay = a{b’} \hfill \cr
bx + {a’}y = {a’}b \hfill \cr} \right.\,\, \Leftrightarrow \,\,\left\{ \matrix{
x = {{a{a’}\left( {{b’} – b} \right)} \over {{a’}{b’} – ab}} \hfill \cr
y = {{b{b’}\left( {{a’} – a} \right)} \over {{a’}{b’} – ab}} \hfill \cr} \right.\)
Vậy \(I\left( {{{a{a’}\left( {{b’} – b} \right)} \over {{a’}{b’} – ab}};\,\,{{b{b’}\left( {{a’} – a} \right)} \over {{a’}{b’} – ab}}} \right)\)
c) Ta có \(C(a\,,\,b)\,;\,\,{C’}({a’}\,,\,{b’})\)
\(\overrightarrow {CI} = \left( { – {{ab\left( {{a’} – a} \right)} \over {{a’}{b’} – ab}}; – {{ab\left( {{b’} – b} \right)} \over {{a’}{b’} – ab}}} \right) = – {{ab} \over {{a’}{b’} – ab}}\overrightarrow {C{C’}} \)
Suy ra C, C’, I thẳng hàng.
d) C là trung điểm IC’ .
\( \Leftrightarrow \,\,\overrightarrow {CI} + \overrightarrow {C{C’}} = \overrightarrow 0 \,\, \)
Advertisements (Quảng cáo)
\(\Leftrightarrow \,\,\overrightarrow {CI} = – \overrightarrow {C{C’}} \,\, \Leftrightarrow \,\,{{ab} \over {{a’}{b’} – ab}} = 1\,\, \Leftrightarrow \,\,{a’}{b’} = 2ab\)
Bài 6: Trong mặt phẳng tọa độ Oxy cho hai điểm A(3, 4); B( 6, 0)
a) Nhận xét gì về tam giác OAB ? Tính diện tích của tam giác đó.
b) Viết phương trình đường tròn ngoại tiếp tam giác OAB.
c) Viết phương trình đường phân giác trong tại đỉnh O của tam giác OAB.
d) Viết phương trình đường tròn nội tiếp tam giác OAB.
Giải
a) Ta có\(OA = \sqrt {{3^2} + {4^2}} = 5\,\,\,;\,\,\,OB = \sqrt {{6^2} + 0} = 6\,\,;\)
\(AB = \sqrt {{3^2} + {4^2}} = 5\,\)
Tam giác OAB cân tại A. Gọi I là trung điểm của OB ta có I(3, 0) và \(AI = \sqrt {{{(3 – 3)}^2} + {{(0 – 4)}^2}} = 4\) .
Diện tích tam giác OAB bằng \(S = {1 \over 2}.AI.OB = {1 \over 2}.4.6 = 12\) .
b) Đường tròn ngoại tiếp tam giác OAB có dạng
\((C):\,{x^2} + {y^2} + 2ax + 2by + c = 0\)
Vì \(O\,,\,A\,,\,B\,\, \in \,\,(O)\) nên
\(\left\{ \matrix{
c = 0 \hfill \cr
9 + 16 + 6a + 8b + c = 0 \hfill \cr
36\,\,\,\,\,\,\,\, + 12a\,\,\,\,\,\,\,\,\, + c = 0 \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\,\left\{ \matrix{
a = – 3 \hfill \cr
b = – {7 \over 8} \hfill \cr
c = 0 \hfill \cr} \right.\)
Vậy \((C)\,:\,{x^2} + {y^2} – 6x – {7 \over 4}y = 0\) .
c) Phương trình đường thẳng \(OA\,:\,\,\,{x \over 3} = {y \over 4}\,\,\, \Leftrightarrow \,\,4x – 3y = 0\)
Phương trình đường thẳng \(OB\,:\,\,\,y = 0\)
Phương trình các đường phân giác tại đỉnh O của tam giác OAB là:
\(\eqalign{
& {{4x – 3y} \over {\sqrt {{4^2} + {3^2}} }} = \pm {y \over 1}\,\,\, \Leftrightarrow \,\,\,\left[ \matrix{
4x – 3y = 5y\,\,\,\,\,\,\,({d_1}) \hfill \cr
4x – 3y = – 5y\,\,\,\,({d_2}) \hfill \cr} \right. \cr
& \Leftrightarrow \,\,\,\left[ \matrix{
4x – 8y = 0 \hfill \cr
4x + 2y = 0 \hfill \cr} \right.\,\,\,\,\,\,\,\, \Leftrightarrow \,\,\,\left[ \matrix{
x – 2y = 0 \hfill \cr
2x + y = 0 \hfill \cr} \right. \cr} \)
Với \({d_1}:x – 2y = 0\,\,\) ta có \(({x_A} – 2{y_A})({x_B} – 2{y_B}) = – 5.6 = – 30 < 0\) . Vậy A và B khác phía đối với d1 , do đó d1 là đường phân giác trong góc O của tam giác OAB.
d) Vì tam giác OAB cân tại A nên AI là phân giác trong góc A của tam giác OAB , ta có \(\overrightarrow {AI} = (0\,;\, – 4)\) nên x = 3 là phương trình đường thẳng AI.
Tọa độ tâm J của đường tròn nội tiếp tam giác OAB là nghiệm hệ phương trình:
\(\left\{ \matrix{
x = 3 \hfill \cr
x – 2y = 0 \hfill \cr} \right.\,\,\, \Leftrightarrow \,\,\left\{ \matrix{
x = 3 \hfill \cr
y = {3 \over 2} \hfill \cr} \right.\)
Vậy \(J\left( {3\,;\,{3 \over 2}} \right)\) .
Bán kính đường tròn nội tiếp tam giác OAB là
\(r = d(J,\,AO) = {{\left| {4.3 – 3.{3 \over 2}} \right|} \over {\sqrt {{3^2} + {4^2}} }} = {3 \over 2}\)
Vậy phương trình đường tròn nội tiếp của tam giác OAB là \({(x – 3)^2} + {\left( {y – {3 \over 2}} \right)^2} = {9 \over 4}\)

